Cho nửa đường tròn (O) đường kính AB. Lấy C là điểm thuộc (O) và gọi d là tiếp tuyến qua C với (O). Kẻ AE và BF cùng vuông góc với d; CH vuông góc vói AB
a, Chứng minh CE = CF và C H 2 = AE.BF
b, Khi C di chuyển trên một nửa đường tròn, tìm vị trí của điểm C để EF có độ dài lớn nhất

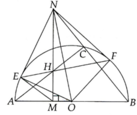
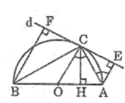
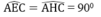
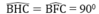
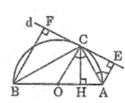
a, Chứng minh được OC là đường trung bình của hình thang AEFB nên C là trung điểm của EF. Chứng minh được AE=AH, BH=BF nên C H 2 = HA.HB = AE.BF
b, Ta có BE ∩ (O) = {H} => FE = AH ≤ AB
=> F E m a x = AB => C là điểm chính giữa AB