Question

[Sennn]

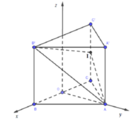
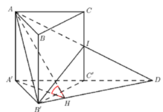
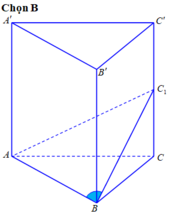
Cho hình lăng trụ đứng có đáy là tam giác đều ABC.A’B’C’ cạnh đáy bằng a. Lấy điểm B1 thuộc BB’ điểm C1 thuộc CC’. Đặt BB1 = x; CC1 = y.
a. Chứng minh rằng tam giác AB1C1 vuông tại B1 khi 2xy = 2x^2 + a^2.
b. Giả sử tam giác AB1C1 là tam giác thường và B1 là trung điểm của BB’ và alpha là góc giữa hai mặt phẳng (ABC) và (AB1C1), cho y = 2x. Tính diện tích tam giác AB1C1 và độ dài cạnh bên của lăng trụ đã cho theo a và alpha.

giúp em với ạ em cảm ơn nhiềuuuu

Answer 1

[Nguyễn Việt Lâm]

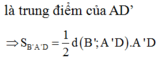
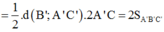
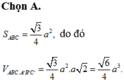
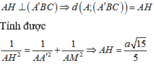
\(2x\left(y-x\right)=a^2>0\Rightarrow y>x\)

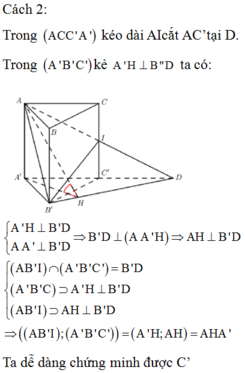
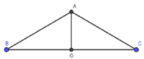
Qua \(B_1\) kẻ đường thẳng song song BC cắt \(CC'\) tại D \(\Rightarrow DC_1=y-x\) và \(B_1D=BC=a\)

Áp dụng Pitago ta có:

\(AC_1^2=AC^2+AC_1^2=a^2+y^2\)

\(AB_1^2=AB^2+BB_1^2=a^2+x^2\)

\(B_1C_1^2=B_1D^2+DC_1^2=a^2+\left(y-x\right)^2\)

\(\Rightarrow AB_1^2+B_1C_1^2=2a^2+x^2+\left(y-x\right)^2=2a^2+2x^2+y^2-2xy\)

\(=2a^2+2x^2+y^2-\left(2x^2+a^2\right)=a^2+y^2=AC_1^2\)

\(\Rightarrow\Delta AB_1C_1\) vuông tại \(B_1\)  theo Pitago đảo.

b.

Do \(B_1\) là trung điểm BB' \(\Rightarrow x=\dfrac{BB'}{2}\), mà \(y=2x\Rightarrow y=BB'\Rightarrow C_1\) trùng C' 

Do \(CC',B_1B\) vuông góc mặt đáy \(\Rightarrow\) tam giác ABC là hình chiếu vuông góc của tam giác \(AB_1C_1\) lên (ABC)

Theo công thức diện tích hình chiếu:

\(S_{ABC}=S_{AB_1C_1}.cos\alpha\Rightarrow S_{AB_1C_1}=\dfrac{S_{ABC}}{cos\alpha}=\dfrac{a^2\sqrt{3}}{4cos\alpha}\)

Gọi D là trung điểm AC' (hay \(AC_1\)) và  E là trung điểm AC

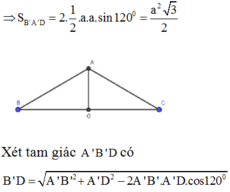
\(\Rightarrow\) \(BEDB_1\) là hình chữ nhật \(\Rightarrow B_1D=BE=\dfrac{a\sqrt{3}}{2}\)

\(B_1C'=B_1A=\sqrt{a^2+\left(\dfrac{x}{2}\right)^2}\) nên tam giác \(AB_1C'\) cân tại \(B_1\Rightarrow B_1D\) đồng thời là đường cao

\(\Rightarrow S_{AB_1C_1}=\dfrac{1}{2}B_1D.AC'=\dfrac{a^2\sqrt{3}}{4cos\alpha}\Rightarrow AC'=\dfrac{a^2\sqrt{3}}{2cos\alpha.B_1D}=\dfrac{a}{cos\alpha}\)

\(\Rightarrow AA'=\sqrt{AC'^2-AC^2}=\sqrt{\dfrac{a^2}{cos^2\alpha}-a^2}=a.tan\alpha\)

Answer 2

[Nguyễn Việt Lâm]