Cho hình thang cân ABCD AB // CD ) có BD vuông góc với BC ; BD là phân giác góc D .
a, chứng minh góc BCD = 2 BDC
b, Tính số đo các góc của hình thang
c, Với BC = 3cm . Tính chu vi và diện tích hình thang
GIÚP MK VS MN ƠI !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 6 2021
Kẻ \(AH;BK\) vuông góc với DC (H,K thuộc DC)
Xét \(\Delta\) AHD và \(\Delta\)BKC:
\(\widehat{AHD}=\widehat{BKC}=90^0\)
AD=BC( do ABCD là hình thang cân)
\(\widehat{D}=\widehat{C}\) (Hai góc cùng kề một đáy trong htc)
nên \(\Delta\)AHD=\(\Delta\)BKC(ch-gn) \(\Rightarrow DH=KC\)
Có AB//DC và AH//BK => ABKH là hbh => AB=HK
Có \(DH+HK+KC=DC\) \(\Leftrightarrow2KC+AB=DC\Leftrightarrow KC=\dfrac{50-14}{2}=18\) (cm)
Áp dụng hệ thức trong tam giác vuông CDB có:
\(BK^2=DK.KC\Leftrightarrow BK=\sqrt{DK.KC}=\sqrt{\left(DC-KC\right).KC}=24\) (cm)
Diện tích hình thang là: \(S=\dfrac{1}{2}BK\left(AB+CD\right)=\dfrac{1}{2}.24\left(14+50\right)=768\) (cm2)
CM
10 tháng 1 2018
a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2
18 tháng 9 2020
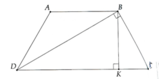
Vì ABCD là hình thang cân nên \(AD=BC,\widehat{ADC}=\widehat{BCD}\)
Xét 2 tam giác ADC và BCD có: DC chung, \(\widehat{ADC}=\widehat{BCD}\), AD=BC
\(\Rightarrow\Delta ADC=\Delta BCD\left(c.g.c\right)\Rightarrow\widehat{DAC}=\widehat{CBD}=90^0\Rightarrow AC\perp AD\)
N
0