Cho ΔABC cân tại a, có AB = 5cm; BC=6cm, tia phân giác AD của \(\widehat{BAC}\) cắt đường trung tuyến BE của tam giác tại G. Tia CG cắt AB tại F.
a. So sánh số đo của \(\widehat{ABC}\) và \(\widehat{BAC}\)
b. ΔABD = ΔACD
c. C/m F là trung điểm của AB
d. Tính độ dài BG

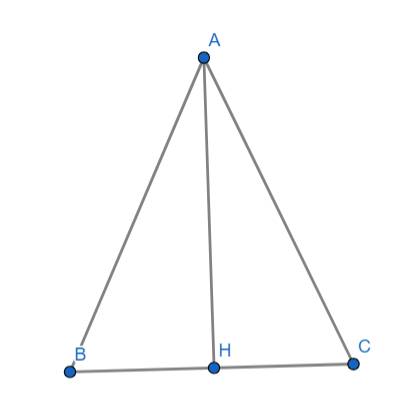
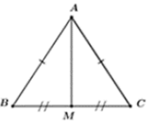

a) ta có: tam giác ABC cân tại A
=> AB = AC = 5 cm ( định lí tam giác cân)
=> AC = 5 cm
=> AC < BC ( 5 cm < 6 cm)
\(\Rightarrow\widehat{ABC}< \widehat{BAC}\) ( quan hệ cạnh và góc đối diện)
b) Xét tam giác ABD và tam giác ACD
có: AB = AC (gt)
góc BAD = góc CAD (gt)
AD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
c) Xét tam giác ABC cân tại A
có: AD là đường phân giác góc BAC (gt)
=> AD là đường trung tuyến của BC ( tính chất trong tam giác cân)
mà BE là đường trung tuyến của AC (gt)
AD cắt BE tại G (gt)
=> G là trọng tâm của tam giác ABC ( định lí trọng tâm)
=> CF là đường trung tuyến của AB ( định lí )
=> AF = BF ( định lí đường trung tuyến)
d) Xét tam giác ABC cân tại A
có: AD là đường phân giác của góc BAC (gt)
=> AD là đường cao ứng với cạnh BC ( tính chất tam giác cân)
\(\Rightarrow AD\perp BC⋮D\) ( định lí đường cao)
mà AD là đường trung tuyên của BC ( phần c)
=> BD = CD = BC/2 = 6/2 = 3 cm
=> BD = 3cm
Xét tam giác ABD vuông tại D
có: \(BD^2+AD^2=AB^2\left(py-ta-go\right)\)
thay số: \(3^2+AD^2=5^2\)
\(AD^2=5^2-3^2\)
\(AD^2=16\)
\(\Rightarrow AD=4cm\)
mà G là trọng tâm của tam giác ABC
AD là đường trung tuyến của BC
\(\Rightarrow\frac{DG}{AD}=\frac{1}{3}\Rightarrow\frac{DG}{4}=\frac{1}{3}\Rightarrow DG=\frac{4}{3}cm\)
Xét tam giác DGB vuông tại D
có: \(DG^2+BD^2=BG^2\left(py-ta-go\right)\)
thay số: \(\left(\frac{4}{3}\right)^2+3^2=BG^2\)
\(BG^2=\frac{97}{9}\)
\(\Rightarrow BG=\sqrt{\frac{97}{9}}cm\)
mk ko bít kẻ hình trên này, sorry bn nhiều nhé!