Question

[Phan Cao Gia Thảo]

Cho ABC vuông tại A có đường cao AH. a) Chứng minh HAC ഗ ABC. b) Tính độ dài đoạn thẳng AC, biết CH = 4cm; BC = 13cm

c) Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua H và vuông góc với HE cắt cạnh AC tại F. Chứng minh AE.CH = AH.FC.

d) Tìm vị trí của điểm E trên cạnh AB để tam giác HEF có diện tích nhỏ nhất.

Answer 1

[Trần Tuấn Hoàng]

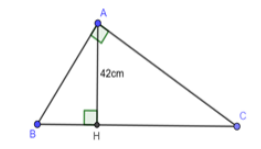
a) -△ABC và △HAC có: \(\widehat{BAC}=\widehat{AHC}=90^0\); \(\widehat{C}\) là góc chung.

\(\Rightarrow\)△ABC∼△HAC (g-g) 

b)\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\Rightarrow AC^2=BC.CH=13.4=52\Rightarrow AC=\sqrt{52}\left(cm\right)\)

c) \(\widehat{AHE}=90^0-\widehat{AHF}=\widehat{CHF}\).

-△AHE và △CHF có: \(\widehat{AHE}=\widehat{CHF}\); \(\widehat{HAE}=\widehat{HCF}\) (△ABC∼△HAC)

\(\Rightarrow\)△AHE∼△CHF (g-g) \(\Rightarrow\dfrac{AH}{CH}=\dfrac{AE}{CF}\Rightarrow AE.CH=AH.FC\).

Answer 2

[Trần Tuấn Hoàng]

d) -Gọi G là giao của AB và HF.

-△GAF và △GHE có: \(\widehat{GAF}=\widehat{GHE}=90^0\); \(\widehat{G}\) là góc chung.

\(\Rightarrow\)△GAF∼△GHE (g-g) \(\Rightarrow\dfrac{GA}{GH}=\dfrac{GF}{GE}\Rightarrow\dfrac{GA}{GF}=\dfrac{GH}{GE}\)

-△GEF và △GHA có: \(\dfrac{GA}{GF}=\dfrac{GH}{GE}\); \(\widehat{G}\) là góc chung.

\(\Rightarrow\)△GEF∼△GHA (c-g-c) \(\Rightarrow\widehat{GFE}=\widehat{GAH}\).

\(\widehat{GAH}=90^0-\widehat{CAH}=\widehat{ACB}\Rightarrow\widehat{GFE}=\widehat{ACB}\).

-△HEF và △ABC có: \(\widehat{EHF}=\widehat{BAC}=90^0;\widehat{HFE}=\widehat{ACB}\).

\(\Rightarrow\)△HEF∼△ABC (g-g) \(\Rightarrow\dfrac{S_{HEF}}{S_{ABC}}=\dfrac{HE}{AB}\Rightarrow S_{HEF}=\dfrac{HE}{AB}.S_{ABC}\)

-Qua H kẻ đg thẳng vuông góc với AB tại E' \(\Rightarrow HE\ge HE'\)

\(\Rightarrow S_{HEF}\ge\dfrac{HE'}{AB}.S_{ABC}\).

-\(S_{HEF}\) có diện tích nhỏ nhất \(\Leftrightarrow E\equiv E'\Leftrightarrow\)E là hình chiếu của H lên AB.