Cho hai điểm cố định A; B. gọi I là trung điểm của AB. Tập hợp các điểm M thoả: M A → + M B → = M A → - M B → là:
A. Đường tròn đường kính AB.
B. Trung trực của AB.
C. Đường tròn tâm I, bán kính AB.
D. Nửa đường tròn đường kính AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B M I C D d
Gọi AC,BD lần lượt là tiếp tuyến kẻ từ A,B tới đường tròn (M). Theo giả thiết thì AC // BD.
Ta có AC vuông góc MC, AC // BD => MC vuông góc BD. Mà MD vuông góc BD nên C,M,D thẳng hàng
Suy ra CD là đường kính của (M) => ^CID chắn nửa đường tròn (M) => ^CID = 900
Hay IC vuông góc ID (1). Ta lại có AI,AC là tiếp tuyến từ A tới (M) => AM là trung trực của IC
=> AM vuông góc IC (2). Tương tự BM vuông góc ID (3)
Từ (1),(2),(3) suy ra MA vuông góc MB => ^AMB = 900 => M nằm trên đường tròn đường kính AB
Do A,B cố định nên đường tròn (AB) cố định. Vậy M luôn di động trên (AB) cố định (đpcm).
Lưu ý: Điểm I cố định hay di chuyển cũng không ảnh hưởng tới kết quả của bài toán.

Chọn D.
Phương pháp: Đây là câu hỏi về kiến thức cơ bản.
Cách giải: Dễ thấy điểm M thuộc mặt nón đỉnh A trục AB và góc ở đỉnh là 60 °

Hướng dẫn: D
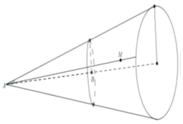
Từ A kẻ đường thẳng d tạo với AB một góc 30 0 ta quay đường thẳng vừa tạo quanh AB với góc 30 0 không đổi thì thu được hình nón.
Lấy điểm K bất kì trên mặt nón đó, ta có K A B ^ = 30 0
Do A, B cố định ⇒ mặt nón cố định
Như vậy K ≡ M là thỏa mãn yêu cầu. Tức quỹ tích điểm M thuộc một mặt nón cố định nhận A làm đỉnh, có đường cao AB trùng với và góc giữa đường sinh và tia AB bằng 30 0 .

- Kẻ đường kính BB’ .Nếu H là trực tâm của tam giác ABC thì AH=B’C. Do C,B’ cố định , cho nên B’C là một véc tơ cố định \(\overrightarrow{\Rightarrow AH}=\overrightarrow{B'C}\)
Theo định nghĩa về phép tịnh tiến điểm A đã biến thành điểm H . Nhưng A lại chạy trên (O;R) cho nên H chạy trên đường tròn (O’;R) là ảnh của (O;R) qua phép tịnh tiến dọc theo \(\overrightarrow{v}=\overrightarrow{B'C}\)
- Cách xác định đường tròn (O’;R) . Từ O kẻ đường thẳng song song với B’C . Sau đó dựng véc tơ : \(\overrightarrow{OO'}=\overrightarrow{B'C}\). Cuối cùng từ O’ quay đường tròn bán kính R từ tâm O’ ta được đường tròn cần tìm .

Đường tròn c: Đường tròn qua B_1 với tâm O Đoạn thẳng g: Đoạn thẳng [A, B] Đoạn thẳng i: Đoạn thẳng [C, D] Đoạn thẳng j: Đoạn thẳng [A, C] Đoạn thẳng k: Đoạn thẳng [C, O] Đoạn thẳng n: Đoạn thẳng [O, J] Đoạn thẳng p: Đoạn thẳng [A, J] O = (1.28, 3.2) O = (1.28, 3.2) O = (1.28, 3.2) Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm C: Giao điểm của c, f Điểm C: Giao điểm của c, f Điểm C: Giao điểm của c, f Điểm M: Điểm trên g Điểm M: Điểm trên g Điểm M: Điểm trên g Điểm D: Giao điểm của c, h Điểm D: Giao điểm của c, h Điểm D: Giao điểm của c, h Điểm I: Tâm của d Điểm I: Tâm của d Điểm I: Tâm của d Điểm N: Giao điểm của g, k Điểm N: Giao điểm của g, k Điểm N: Giao điểm của g, k Điểm J: Giao điểm của c, m Điểm J: Giao điểm của c, m Điểm J: Giao điểm của c, m
a. Cô sửa thành AM2 = CM.CD
Xét tam giác ACM và DCA có: \(\widehat{C}\) chung, \(\widehat{CAM}=\widehat{CDA}\) (Chắn hai cung CB và CA bằng nhau)
Vậy thì \(\Delta ACM\sim\Delta DCA\left(g-g\right)\Rightarrow\frac{AC}{CD}=\frac{CM}{CA}\Rightarrow CA^2=CD.CM\)
b. C là điểm chính giữa cung AB nên OC vuông góc AB tại trung điểm N. Gọi I là tâm đường tròn ngoại tiếp tam giác ADM. AI cắt (O) tại J.
Do câu a: \(\Delta ACM\sim\Delta DCA\left(g-g\right)\Rightarrow\widehat{CAD}=\widehat{CMA}\)
Lại có \(\widehat{JAD}=\widehat{JCD}\) nên \(\widehat{JAD}+\widehat{DAC}=\widehat{JCD}+\widehat{CMA}=90^o\Rightarrow\widehat{CAJ}=90^o\)
Vậy CJ là đường kính (O) hay J cố định, từ đó suy ra Ạ cố định. Lại có tâm I luôn thuộc AJ nên ta đã chứng minh được tâm đường tròn ngoại tiếp tam giác ADM thuộc một đường thẳng cố định.

a: Xét ΔMCD và ΔMEC có
góc MCD=góc MEC
góc CMD chung
=>ΔMCD đồng dạng với ΔMEC
b: Xét (O) có
MA,MC là tiếp tuyến
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại K
ΔMCO vuông tại C có CK là đường cao
nên MK*MO=MC^2
c: góc AOC=2*góc AIC=120 độ
=>góc AOM=góc COM=60 độ
Xét ΔCOM vuông tại C có tan COM=CM/CO
=>CM/R=căn 3
=>CM=R*căn 3

Đáp án B
+ Để cường độ điện trường tổng hợp tại trung điểm AB bằng 0 thì hai điện tích này phải cùng dấu và cùng độ lớn
Đáp án A