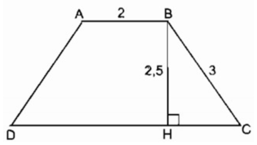
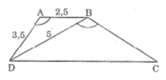
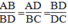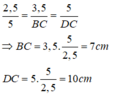Cho hình thang ABCD (AB//CD) biết AB=2,5cm ; AD=3,5cm ; BD=5cm và \(\widehat{DAB}=\widehat{DBC}\)
a, C/m: ΔABD\(\sim\)ΔBDC
b, Tính BC, DC
c, Gọi E là giao điểm của AC và BD. Qua E kẻ đường thẳng bất kì cắt AB, CD lần lượt tại M và N. Tính \(\frac{ME}{NE}\)