Cho hình chóp tứ giác có đáy ABCD là hình chữ nhật có AB = a; AD = 2a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = a 2 . Thể tích V của khối chóp là :
A . V = 2 2 9 a 3
B . V = 2 3 a 3
C . V = 2 2 a 3
D . V = 2 2 3 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
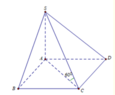
Ta có A ⇔ = a 2 + a 2 2 = a 3
S
A
=
A
C
tan
60
0
=
a
3
.
3
=
3
a
;
S
A
B
C
D
a
.
a
2
=
a
2
2
Thể tích hình chóp S.ABCD là:
V = 1 3 S A . S B A C D = 1 3 .3 a . a 2 2 = a 3 2

Đáp án A
Theo bài ra ta có:
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
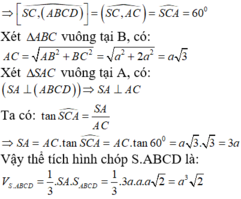

Đáp án D
Dễ thấy ![]()
Lại có ∆SAC vuông tại A
=> AC = SA = ![]()
Vậy VS.ABCD = ![]()

Đáp án A
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
Xét ΔABC vuông tại B, có


Chọn A.
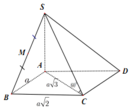
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD)


Đáp án D
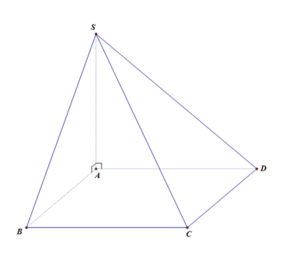
V S . A B C D = 1 3 S A B C D . S A = 1 3 . A B . A D . S A = 1 3 a . 2 a . a 2 = 2 2 a 3 3 .
Đáp án D