ΔABC vuông tại A,Có I là trung điểm Bc.
A)Cho Ab=6cm ; AC=8cm.Tính AI
B) Từ I kẻ IH ⊥ AB ; IK ⊥ AC.Chứng minh tứ giác AHIK là hình chữ nhật.
C)Vẽ E đ/x I qua K. Chứng minh tứ giác AICE là hình thoi
D) Tính diện tích ΔABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2022
a: AI=5cm
b: Xét tứ giác AHIK có
\(\widehat{AHI}=\widehat{AKI}=\widehat{KAH}=90^0\)
Do đó: AHIK là hình chữ nhật
1 tháng 10 2021
Bài 1:
Xét ΔBMC có
N là trung điểm của BM
I là trung điểm của BC
Do đó: NI là đường trung bình của ΔBMC
Suy ra: NI//MK
Xét ΔANI có
M là trung điểm của AN
MK//NI
Do đó: K là trung điểm của AI
31 tháng 12 2021
a: Xét ΔAKB và ΔAKC có
AK chung
KB=KC
AB=AC
Do đó: ΔAKB=ΔAKC
17 tháng 4 2023
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: AD=DH
DH<DC
=>AD<DC
c: Xet ΔDAK vuông tại A và ΔDHC vuông tại H có
DA=DH
góc ADK=góc HDC
=>ΔDAK=ΔDHC
=>DK=DC và AK=HC
=>D nằm trên trung trực của KC(1) và BK=BC
=>ΔBKC cân tại B
mà BI la trung tuyến
nen BI là trung trực của KC(2)
Từ (1), (2) suy ra B,I,D thẳng hàng
11 tháng 2 2021
a) Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC(ΔABC cân tại A)
Do đó: ΔABD=ΔACD(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{BAD}=\widehat{CAD}\)(hai góc tương ứng)
mà tia AD nằm giữa hai tia AB,AC
nên AD là tia phân giác của \(\widehat{BAC}\)(đpcm)
Ta có: ΔABD=ΔACD(cmt)
nên DB=DC(hai cạnh tương ứng)
Ta có: DB=DC(cmt)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Từ (1), (2) và (3) suy ra A,M,D thẳng hàng(đpcm)
9 tháng 4 2023
\(\text{#TNam}\)
`a,`
Xét Tam giác `AIB` và Tam giác `AIC` có:
`AB = AC (\text {Tam giác ABC cân tại A})`
\(\widehat{B}=\widehat{C} (\text {Tam giác ABC cân tại A})\)
`IB = IC (\text {I là trung điểm BC})`
`=> \text {Tam giác AIB = Tam giác AIC (c-g-c)}`
`->`\(\widehat{AIB}=\widehat{AIC} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->` \(\widehat{AIB}+\widehat{AIC}=180^0\)
`->`\(\widehat{AIB}=\widehat{AIC}=\) `180/2=90^0`
`-> Ai \bot BC (đpcm).`
`b,`
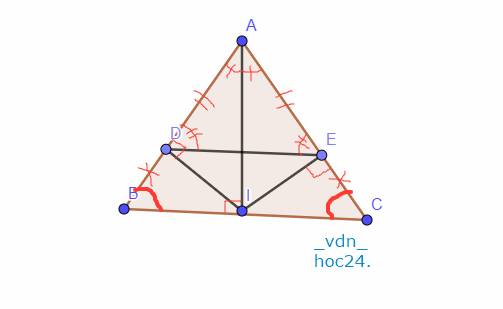
Xét Tam giác `BDI` và Tam giác `CEI` có:
`IB = IC (g``t)`
\(\widehat{B}=\widehat{C} (gt)\)
\(\widehat{BDI}=\widehat{CEI}=90^0\)
`=> \text {Tam giác BDI = Tam giác CEI (ch-gn)}`
`-> BD = CE (\text {2 cạnh tương ứng})`
`c,`
Vì Tam giác `AIB =` Tam giác `AIC (a)`
`->`\(\widehat{BAI}=\widehat{CAI} (\text {2 góc tương ứng})\)
Xét Tam giác `ADI` và Tam giác `AEI` có:
`\text {AI chung}`
\(\widehat{DAI}=\widehat{EAI} (CMT)\)
\(\widehat{ADI}=\widehat{AEI}=90^0\)
`=> \text {Tam giác ADI = Tam giác AEI (ch-gn)}`
`-> AD = AE (\text {2 cạnh tương ứng})`
Xét Tam giác `ADE: AD = AE`
`-> \text {Tam giác ADE cân tại A}`
`->`\(\widehat{ADE}=\widehat{AED}\)\(=\dfrac{180-\widehat{A}}{2}\)
Tam giác `ABC` cân tại `A`
`->`\(\widehat{B}=\widehat{C}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{ADE}=\widehat{B}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {DE // BC (t/c 2 đt' //)}`
17 tháng 12 2021
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
Do đó: ΔABH=ΔACH
a: AI=5cm
b: Xét tứ giác AHIK có
\(\widehat{AHI}=\widehat{AKI}=\widehat{KAH}=90^0\)
Do đó: AHIK là hình chữ nhật