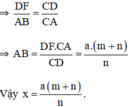Câu 4. (1 điểm) Giữa hai điểm A và B có một cái ao. Để đo khoảng cách AB người ta đo được các đoạn thẳng IA=9m; AC=11m và BD=33m. Biết AC // BD. Tính chiều rộng AB của cái ao.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


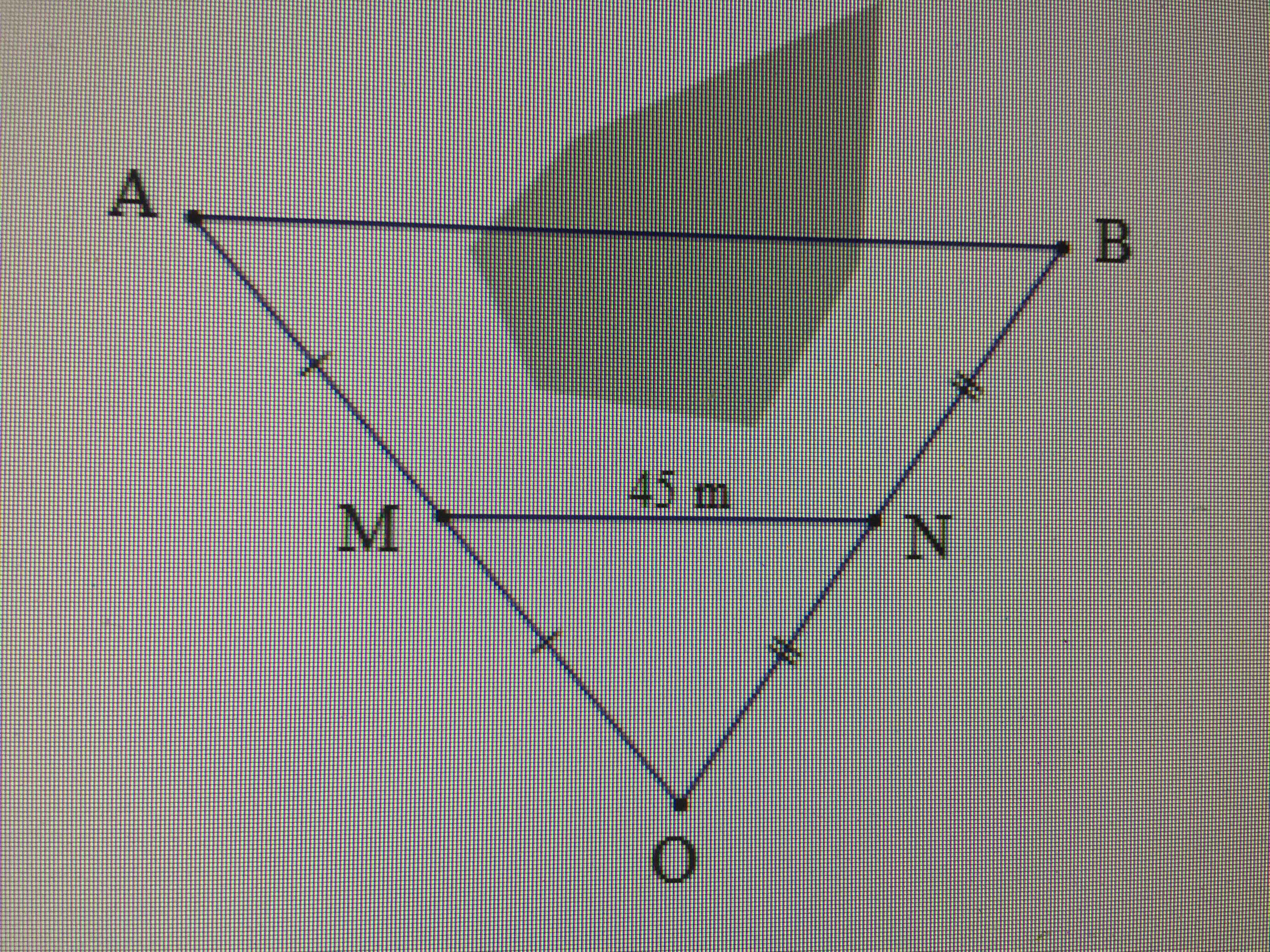
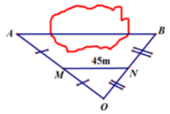
Xét tam giác OAB có:
M là trung điểm AO(gt)
N là trung điểm OB(gt)
=> MN là đường trung bình
\(\Rightarrow AB=2MN=2.45=90\left(m\right)\)

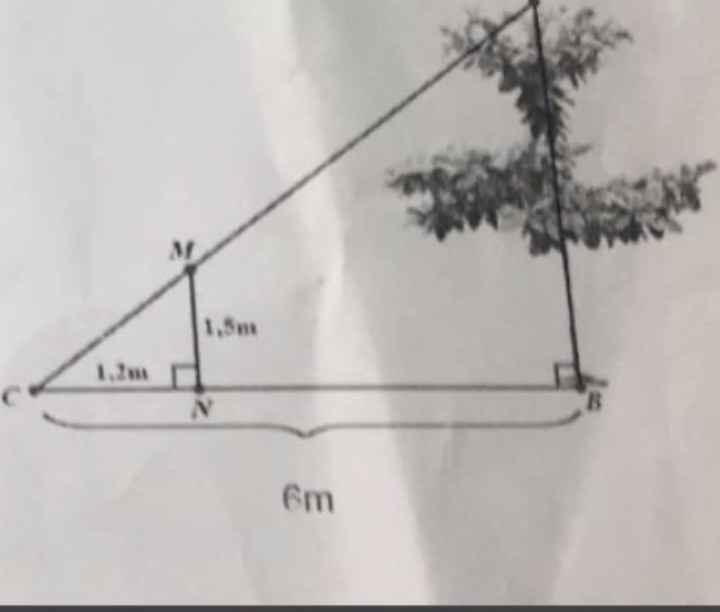
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)

Chọn B.
Áp dụng định lí cosin trong tam giác ta có:
AB2 = AC2 + BC2 - 2BC.AC.cosC
= 2502 + 1202 - 2.250.120.cos78024’ = 64835
Suy ra AB = 255.

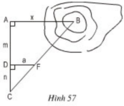
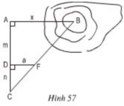
a) Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
b) ΔCDF 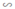 ΔCAB (do DF // AB)
ΔCAB (do DF // AB)
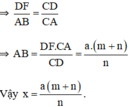

a) Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
b) ΔCDF 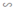 ΔCAB (do DF // AB)
ΔCAB (do DF // AB)