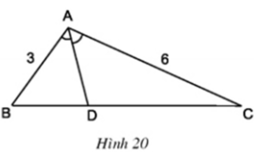
Vẽ tam giác ABC, biết: AB = 3cm

PT

Pham Trong Bach

20 tháng 7 2017

Vẽ tam giác ABC, biết: AB = 3cm; AC = 6cm; ∠A = 100o. Dựng đường phân giác AD của góc A (bằng compa, thước thẳng), đo độ dài các đoạn thẳng DB, DC rồi so sánh các tỉ số A B A C = D B D C (h.20)....

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

20 tháng 7 2017

BD ≈ 2 cm; DC ≈ 4 cm

Để học tốt Toán 8 | Giải toán lớp 8

Đúng(0)

TL

Trân Lê

2 tháng 5 2021

Vẽ tam giác ABC biết BC = 5cm; AB = 3cm; AC= 4cm. Đo góc A của tam giác ABC.

#Toán lớp 6

3

NI

nihaoma2k8 •ᑎIᕼãO ᗰᗩ⁀ᶜᵘᵗᵉ

2 tháng 5 2021

Góc A bằng 90^onghe bạn. Bạn chỉ cần vẽ hình là ra ngay thôi. Vì trong chương trình lớp 7, bạn sẽ hc bộ 3-4-5 là bộ 3 cạnh tam giác vuông.

Đúng(0)

H

heliooo

2 tháng 5 2021

Mình không vẽ hình trên máy tính được nha, nhưng mình biết góc A = 90⁰.

Chúc bạn học tốt!! ^^

Đúng(0)

R

RANI_CHAN

7 tháng 12 2021

vẽ tam giác ABC biết AB =4cm, AC =3cm, BC= 5cm. Vẽ tia phân giác của góc A.

giúp mik với mn

#Toán lớp 7

0

VT

Vũ Thị Phương Uyên

26 tháng 4 2021 - olm

Vẽ tam giác ABC, biết AB= 4cm ; AC= 3cm; BC= 5cm

#Toán lớp 6

3

6N

6 Nguyễn Ngọc Châm

26 tháng 4 2021

bạn thông cảm nha !

máy mik lỗi nên ko gửi ảnh đc

Đúng(0)

YN

Yen Nhi

26 tháng 4 2021

Cách vẽ:

Bước 1: Dùng thước thẳng vẽ cạnh AB dài 5cm

Bước 2: Dùng compa đặt trên thước thẳng sao cho hai đầu của compa cách nhau đúng 4cm

Bước 3: Đặt đầu nhọn của compa vào điểm A rồi vẽ đường tròn thứ nhất

Bước 4: Tiếp tục dùng compa đặt trên thước thẳng sao cho hai đầu của compa cách nhau đúng 3cm

Bước 5: Đặt đầu nhọn của compa vào điểm B rồi vẽ đương tròn thứ hai

Bước 6: Hai đường tròn này cắt nhau tại 2 điểm bạn chọn lấy 1 trong 2 điểm làm điểm C

Bước 7: Nối A với C, B với C ta được tam giác ABC lần lượt có số đo 3 cạnh là 3cm, 4cm, 5cm

Hình vẽ:

B A C

Đúng(0)

TT

Trần Thế Miên An

21 tháng 3 2022

Cho ABC vuông tại A, biết AB =3cm; AC =4cm. a) Tính BC.So sánh các cạnh của tam giác ABC b) Vẽ phân giác BD của góc ABC (D thuộc AC),từ D vẽ DE trung điểm BC(E thuộc BC) c) ED cắt AB tại F.Chứng minh tam giác ADF=tam giác EDC d) Chứng minh AB+AF

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

30 tháng 7 2023

a: BC=căn 3^2+4^2=5cm

b,d: Đề bài yêu cầu gì?

c: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

=>DA=DE

Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

góc ADF=góc EDC

=>ΔDAF=ΔDEC

Đúng(0)

PT

phạm thuý hằng

23 tháng 4 2017 - olm

vẽ tam giác ABC biết AB=3cm,BC=4cm,AC=5cm. ( Nêu cách vẽ).tam giác ABC có đặc điểm gì ?

ai nhanh tk nhớ giải chi tiết nhé

#Toán lớp 6

2

Q

Quang

23 tháng 4 2017

Cách vẽ:

Vẽ AC = 5 cm.

Vẽ cung tròn (A; 3 cm).

Vẽ cung tròn (C; 4 cm).

Hai cung tròn cắt nhau tại B. Vẽ đoạn thẳng BA, BC ta được tam giác ABC.

B A C 5 cm 3 cm 4 cm

Tam giác ABC có 1 góc vuông tại B

Đúng(2)

TL

Trần Linh

23 tháng 4 2017

tam giác ABC là tam giác vuông do:

AC² =AB²+BC² ( ĐỊNH LÝ PY TA GO)

VẬY tam giác ABC vuông tại B

Đúng(0)

UP

Uyên Phan

6 tháng 12 2021

Vẽ tam giác biết hai cạnh và góc xen giữa cạnh của nó (tam giác ABC có AB=3cm ; AC=4cm;góc A=90 độ

#Toán lớp 7

0

TT

Trần Thế Miên An

21 tháng 3 2022

Cho ABC vuông tại A, biết AB =3cm; AC =4cm. a) Tính BC.So sánh các cạnh của tam giác ABC b) Vẽ phân giác BD của góc ABC (D thuộc AC),từ D vẽ DE trung điểm BC(E thuộc BC) c) ED cắt AB tại F.Chứng minh tam giác ADF=tam giác EDC d) Chứng minh AB+AF

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

31 tháng 7 2023

a: BC=căn 3^2+4^2=5cm

AB<AC<BC

=>góc C<góc B<góc A

c: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

=>DA=DE

Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

góc ADF=góc EDC

=>ΔDAF=ΔDEC

Đúng(0)

NV

Nguyễn Vũ Bảo Ngọc

10 tháng 11 2017 - olm

Cho tam giác ABC và tam giác ABD biết :

AB=BC=3cm(và D nằm khác phía đối với AB)

a)Vẽ tam giác ABC và tam giác ABD (AD=BD=2cm)

b)Chứng minh AD=BD

#Toán lớp 7

0

TL

Trân Lê

2 tháng 5 2021

Vẽ tam giác ABC biết độ dài ba cạnh là AB=3m, AC=3cm, BC=4cm (Học sinh phải nêu cách vẽ)

#Toán lớp 6

1

MP

Minh Phương

2 tháng 5 2021

Vẽ BC=4CM ,TỪ TRUNG ĐIỂM CỦA BC ,KẺ ĐOẠN THẲNG VUÔNG GÓC VỚI BC. SAU ĐÓ TỪ B kẻ đoạn AB=3cm cắt đường vuông góc với BC tại A, từ C kẻ đoạn AC=3cm cắt đường vuông góc với BC tại A

Đúng(0)

J

JEsusDownstair

16 tháng 10 2021

Cho tam giác ABC vuông tại B có đường cao BE . Biết AB = 3cm, AC = 6cm.
a) Giải tam giác vuông ABE
b) Tính AE, BE, CE
c) Vẽ đường phân giác AM của tam giác ABC, tính AM, MB, MC

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

16 tháng 10 2021

b: Xét ΔABC vuông tại B có

\(BA^2+BC^2=AC^2\)

hay \(BC=3\sqrt{3}\left(cm\right)\)

Xét ΔABC vuông tại B có BE là đường cao ứng với cạnh huyền AC

nên \(\left\{{}\begin{matrix}BA^2=AE\cdot AC\\BC^2=CE\cdot CA\\BE\cdot AC=BA\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AE=1.5\left(cm\right)\\CE=4.5\left(cm\right)\\BE=\dfrac{3\sqrt{3}}{2}\left(cm\right)\end{matrix}\right.\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP