Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Làm tiếp nha:
Xét tứ giác ABEC có 2 đường chéo AE và BC cắt nhau tại trung điểm M của mỗi đường nên ABEC là hình bình hành.
=> \(\hept{\begin{cases}AB=CE\left(1\right)\\ABllCE\end{cases}}\)
a ) xét \(\Delta ABM\)và \(\Delta ECM\)có:
\(\hept{\begin{cases}MA=ME\left(gt\right)\\MB=MC\left(gt\right)\\AB=CE\left(cmt\right)\end{cases}}\)
---> \(\Delta ABM=\Delta ECM\left(c.c.c\right)\)
b) Xét \(\Delta ABD\) có BH là đường cao đồng thời đường trung tuyến nên \(\Delta ABD\) cân tại B.
---> BC là phân giác của ABD
\(\Delta ABD\)cân tại B ---> AB = BD (2)
Từ (1),(2) ---> BD = CE
Xét tứ giác ABEC có 2 đường chéo AE và BC cắt nhau tại trung điểm M của mỗi đường nên ABEC là hình bình hành
\(\Rightarrow\begin{cases}AB=CE\left(1\right)\\AB\backslash\backslash CE\end{cases}\)
a,xét ΔABM và ΔECM có:
\(\begin{cases}MA=ME\left(gt\right)\\MB=MC\left(gt\right)\\AB=CE\left(cmt\right)\end{cases}\)
→ΔABM=ΔECM(c.c.c)
b,Xét ΔABD có BH là đường cao đồng thời là đường trung tuyến
nên ΔABD cân tại B
→BC là phân giác của \(\widehat{ABD}\)
ΔABD cân tại B →AB=BD(2)
Từ (1),(2)→BD=CE
Mjk tra loi cau a nka
B C M K
Mjk ve hoi xau, pn thong cam nka
Vì tam giác ABM và ACM có:
M1=M2(đối đỉnh dok pn)
AM=MK(gt)
BM=MC( gt)
=> tam giác ABM=tam giác ACM(c.g.c)
k ve dc tam giac nho nen mjk phai ghi la tam giac lun ak
a) Xét ∆ABM và ∆CME ta có :
BM = MC ( M là trung điểm BC)
AM = ME
AMB = CME ( đối đỉnh)
=> ∆ABM = ∆CME(c.g.c)
b) Xét ∆AMC và ∆BME ta có :
AM = ME
BM = MC
AMC = BME ( đối đỉnh)
=> ∆AMC = ∆BME(c.g.c)
=> ACM = MBE
Mà 2 góc này ở vị trí so le trong
=> AC//BE
c) Vì ∆AMB = ∆CME
=> ABC = BCK
Xét ∆IMB và ∆CMK ta có :
BM = MC
BI = CK
ABC = BCE (cmt)
=> ∆IMB = ∆CMK (c.g.c)
=> IMB = CMK
Ta có :
BMI + IMC = 180° ( kề bù)
Mà IMB = CMK
=> CMK + IMC = 180°
=> IMK = 180°
=> IMK là góc bẹt
=> I , M , K thẳng hàng
`a,`
Xét `\Delta AMC` và `\Delta EMB`:
\(\left\{{}\begin{matrix}\text{MB = MC (M là trung điểm của BC)}\\\widehat{\text{AMC}}=\widehat{\text{BME}}\left(\text{đối đỉnh}\right)\\\text{MA = ME (gt)}\end{matrix}\right.\)
`=> \Delta AMC = \Delta EMB (c-g-c)`
`b,`
Vì `\Delta AMC = \Delta EMB (a)`
`->` $\widehat {ACM} = \widehat {EBM} (\text {2 góc tương ứng})$
Mà `2` góc này nằm ở vị trí sole trong
`->` \(\text{AC // BE (tính chất 2 đường thẳng //)}\)
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC và AB=EC
c: Xét ΔBCD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔBCD cân tại C
d: Xét ΔOBC có
OM là đường cao
OM là đường trung tuyến
Do đó: ΔOBC cân tại O
Suy ra: OB=OC(1)
Xét ΔOBD có
OA là đường cao
OA là đường trung tuyến
Do đó: ΔOBD cân tại O
Suy ra: OB=OD(2)
Từ (1) và (2) suy ra OB=OC=OD
hay O cách đều ba đỉnh của ΔBDC
tham khảo Câu hỏi của huỳnh thị tuyết như - Toán lớp 7 - Học toán với OnlineMath
a, Xét tam giác ABM và tam giác ECM có : góc AMB= góc EMC (2 góc đối đỉnh)
MA=ME (gt)
MB =MC (gt)
Nên tam giác ABM = tam giác ECM (c-g-c)
b, Vì tam giác ABM = tam giác ECM (cm câu a) nên góc ABM = góc ECM (2 góc tương ứng )
Mà góc ABM và góc ECM ở vị trí so le trong nên AB // CE
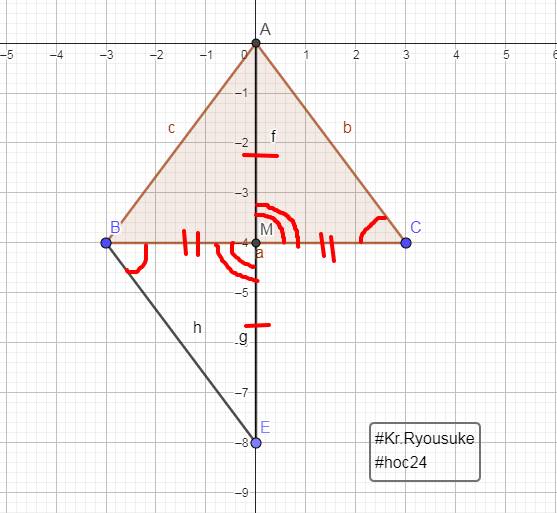
(Bạn tự vẽ hình giùm)
a) Mình xin chỉnh lại đề:
Chứng minh: AC = BE; AC // BE
\(\Delta AMC\)và \(\Delta BME\)có: BM = MC (M là trung điểm BC)
\(\widehat{AMC}=\widehat{BME}\)(đối đỉnh)
AM = ME (gt)
=> \(\Delta AMC\)= \(\Delta BME\)(c - g - c) => AC = BE (hai cạnh tương ứng)
và \(\widehat{ACM}=\widehat{EBM}\)(hai góc tương ứng) ở vị trí so le trong => AC // BE (đpcm)
c) Ta có \(\widehat{BME}=180^o-\widehat{EBM}-\widehat{BEM}\)(tổng ba góc của một tam giác)
=> \(\widehat{BME}\)= 180o - 50o - 25o = 105o
và \(\widehat{HBE}+\widehat{HEB}=90^o\) (\(\Delta BEH\)vuông tại H)
=> 50o + \(\widehat{HEB}\)= 90o
=> \(\widehat{HEB}=40^o\)
=> \(\widehat{MEB}+\widehat{HEM}=40^o\)
=> 25o + \(\widehat{HEM}\)= 40o
=> \(\widehat{HEM}\)= 15o