Cho ∆ABC buông tại A; AB=6cm,AC=8cm,M là trung điểm của BC. Trên tai đối của tia MA lấy điểm D dao cho MD=Ma a/ tính AM b/CM: AB//CD c/AB+AC>2AM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hình bạn tự vẽ nha
a) Vì \(MI⊥AC\)tại I
\(BC⊥AC\)tại C
=>MI // BC
b) Vì \(MK⊥BC\)tại K
\(AC⊥BC\)tại C
=> MK // AC
c) Vì MI // CB
=> \(\widehat{AMI}=\widehat{ABC}=60độ\)( 2 góc đồng vị) ; \(\widehat{IMK}+\widehat{CKM}=180độ\)
\(\widehat{IMK}+90độ=180độ\)
\(\widehat{IMK}=90độ\)
Xét tam giác MKB vuông tại K có:
\(\widehat{KBM}+\widehat{KMB}=90độ\)
\(60độ+\widehat{BMK}=90độ\)
\(\widehat{BMK}=30độ\)
Vậy \(\widehat{IMK}=90độ;\widehat{AIM}=60độ;\widehat{KMB}=30độ\)

Dễ thấy A=3cm
20s dao động 50 lần => 1s dao động 2,5 lần hay f=2,5 => ω=2.pi.f = 5pi
tương tự câu 1 : ω= căn (g/Δℓo) => Δℓo = 0,04m = 4cm > 3cm
=> điểm mà lò xo không giãn nằm trên biên trên và vị trí cân bằng
vẽ hình => Δℓ[min] = 4-3=1cm, Δℓ[max] = 4+3+3=10cm
tỉ số lực đàn hồi cực đại và cực tiểu : Δℓ[max] / Δℓ[min]=10

Lần đầu kéo dãn lò xo một đoạn A rồi buông nhẹ → vật sẽ dao động với biên độ bằng A.
Thời điểm gần nhất động năng bằng thế năng kể từ lúc thả là ∆ t = T 8 và vị trí x0 có động năng bằng thế năng tương ứng là
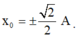
Lần thứ hai. Thời điểm vật đi qua vị trí x0 là
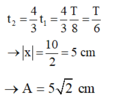
Trong lần đầu, sau khi đi được quãng đường 2A vật sẽ đến vị trí lò xo bị nén cực đại.
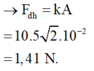
Đáp án B

Đáp án B
+ Lần đầu kéo dãn lò xo một đoạn A rồi buông nhẹ → vật sẽ dao động với biên độ bằng A.
Thời điểm gần nhất động năng bằng thế năng kể từ lúc thả là ∆ t = T 8 và vị trí x 0 có động năng bằng thế năng tương ứng là:
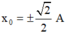
+ Lần thứ hai. Thời điểm vật đi qua vị trí x 0 là:
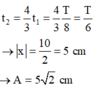
+ Trong lần đầu, sau khi đi được quãng đường 2A vật sẽ đến vị trí lò xo bị nén cực đại.
![]()