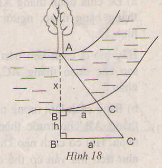
Để đo chiều cao của một cái cây người ta dựng hình vẽ và tiến hành đo đạc các đoạn B'C'=1,5m ; AB'=2m , B'B=8m. Tính chiều cao của cái cây.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
= mà AB' = x + h nên
= <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng

Ta có hình như sau :
giải :
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
Ta có hình như sau :

Giải
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng

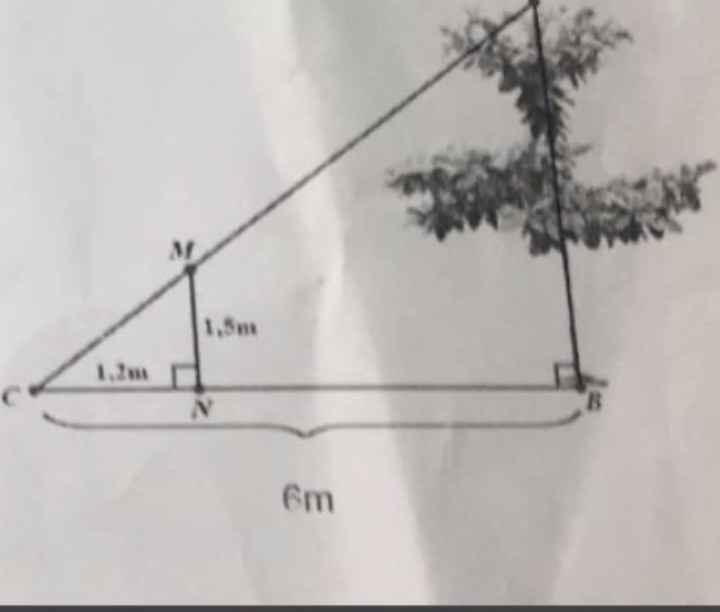
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)

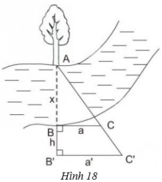
+ Mô tả cách làm:
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 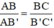 (hệ quả định lý Talet)
(hệ quả định lý Talet)
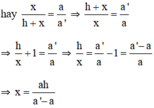

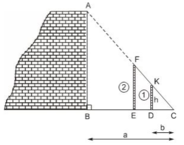
a) Cách tiến hành:
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A, F, K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).
b) ΔABC có AB // KD (D ∈ BC, K ∈ AC)
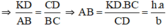
Vậy chiều cao bức tường là 

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)
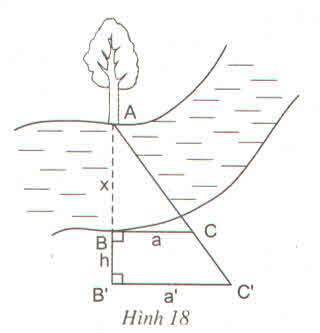
Ta có : vì B'C' // BC
=> \(\dfrac{AB'}{B'B}=\dfrac{B'C'}{BC}< =>\dfrac{2}{8}=\dfrac{1,5}{BC}< =>BC=6\)
Vậy cái cây cao 6m