Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật
A
B
=
a
;
A
D
=
a
3
2
.
Mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng. Biết
A
S
B
⏜
=
120
∘
. Góc giữa hai mặt phẳng (SAD) và (SBC) bằng: A.
60
∘
B.
30
∘
C.
45
∘
D.
90
∘
...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật A B = a ; A D = a 3 2 . Mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng. Biết A S B ⏜ = 120 ∘ . Góc giữa hai mặt phẳng (SAD) và (SBC) bằng:
A. 60 ∘
B. 30 ∘
C. 45 ∘
D. 90 ∘
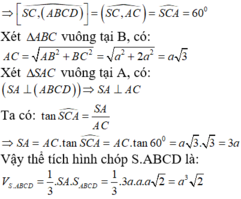
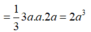
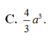
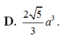
Đáp án A
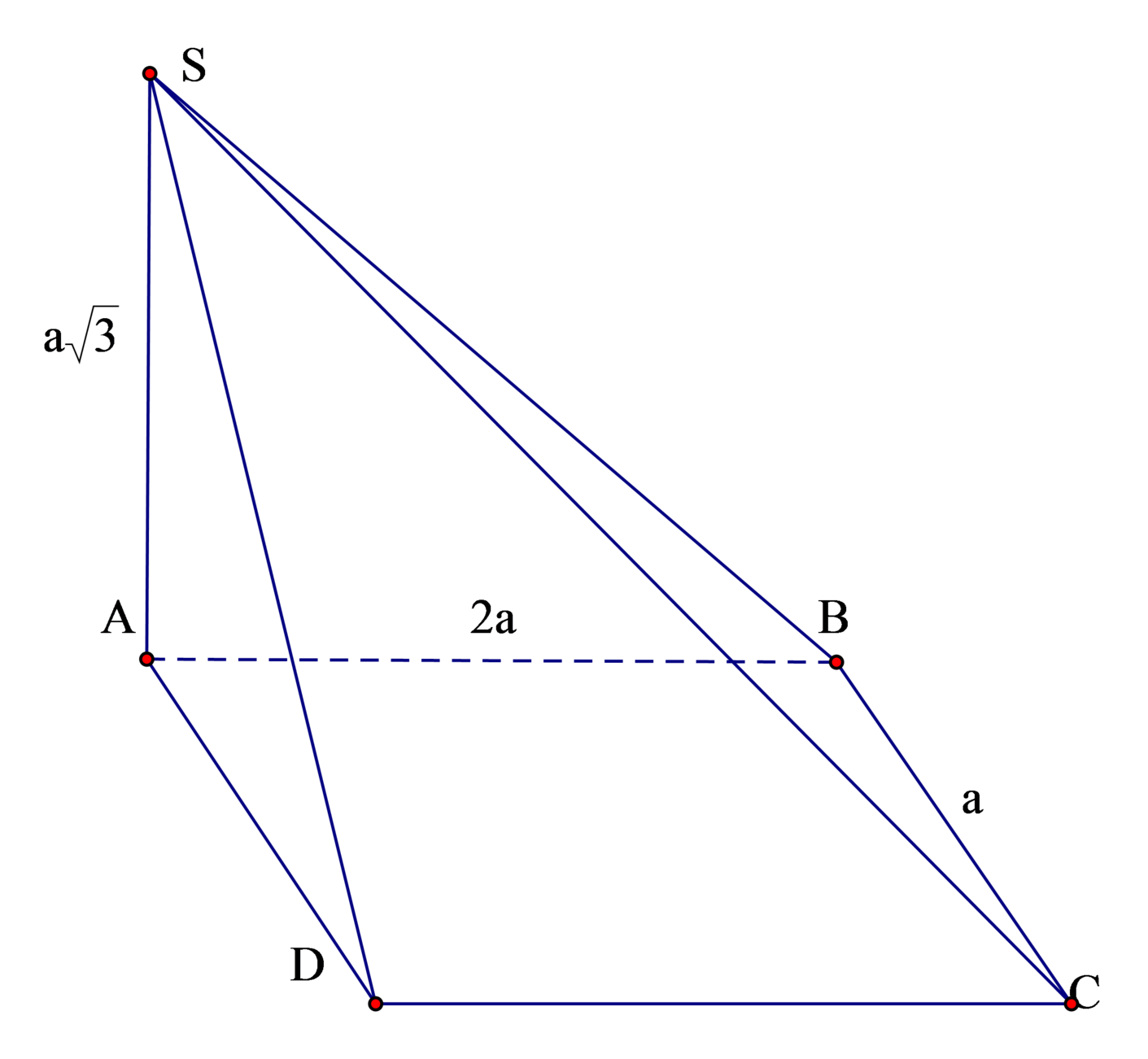
Gọi H là trung điểm của AB .
Lại có: S A B ⊥ A B C D ⇒ S H ⊥ A B C D .
Do A D / / B C nên giao tuyến d của (SAD) và (SBC) đi qua S và song song với AD.
Do A D ⊥ A B A D ⊥ S H ⇒ A D ⊥ S A B ⇒ d ⊥ S A B .Suy ra góc giữa hai mặt phẳng (SAD) và (SBC) bằng 180 ∘ − AS B ⏜ = 60 ∘ .