Cho △ A B C có A B + A C = 10 c m ; A C − A B = 4 c m . So sánh B ^ và C ^
A. C ^ < B ^
B. C ^ > B ^
C. C ^ = B ^
D. B ^ < C ^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
29 tháng 9 2017
Đúng(0)
Những câu hỏi liên quan
NT
1
8 tháng 10 2016
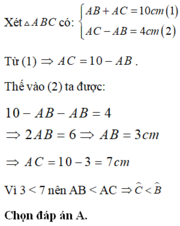
Ta có :
\(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}=\frac{1}{10}\)
\(\Rightarrow2017\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)=2017.\frac{1}{10}\)
\(\Rightarrow\frac{2017}{a+b}+\frac{2017}{b+c}+\frac{2017}{c+a}=201,7\)
Mà \(2017=a+b+c\)nên :
\(\Rightarrow\frac{a+b+c}{a+b}+\frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}=201,7\)
\(\Rightarrow\left(\frac{a+b}{a+b}+\frac{c}{a+b}\right)+\left(\frac{b+c}{b+c}+\frac{a}{b+c}\right)+\left(\frac{a+c}{a+b}+\frac{b}{a+c}\right)=201,7\)
\(3+\frac{c}{a+b}+\frac{a}{b+c}+\frac{b}{c+a}=201,7\)
\(\Leftrightarrow M=\frac{c}{a+b}+\frac{a}{b+c}+\frac{b}{c+a}=201,7-3\)
\(\Leftrightarrow M=198,7\)
Vậy ...
PT
2
21 tháng 11 2017
Vì a+b +c khác 0 và a/b =b/c =c/a
theo tính chất dãy tỉ số bằng nhau
a/b =b/c =c/a = (a+b+c)/( b +c +a) =1 ( vì a+b +c khác 0)
suy ra a=b=c
M= a10+7+2000/a2017=1
S
21 tháng 11 2017
ÁP dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\left(a+b+c\ne0\right)\)
=> a/b = 1 => a = b (1)
b/c = 1 => b = c (2)
c/a = 1 => c = a (3)
Từ (1),(2),(3) => a=b=c
Vậy \(M=\frac{a^{10}.b^7.c^{2000}}{b^{2017}}=\frac{b^{10}.b^7.b^{2000}}{b^{2017}}=\frac{b^{2017}}{b^{2017}}=1\)
NT
0
ND
0
4 tháng 9 2018
a) ta có: \(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1.\)
\(\Rightarrow\frac{a}{b}=1\Rightarrow a=b\); b/c = 1 => b = c
=> a = b = c
\(\Rightarrow M=\frac{a^{10}.b^7.c^{2000}}{b^{2017}}=\frac{b^{10}.b^7.b^{2000}}{b^{2017}}=1\)
4 tháng 9 2018
b) ta có: \(\frac{a+b-c}{c}=\frac{a-b+c}{b}=\frac{-a+b+c}{a}=\frac{a+b-c+a-b+c-a+b+c}{c+b+a}=\frac{a+b+c}{a+b+c}=1\)
\(\Rightarrow\frac{a+b-c}{c}=1\Rightarrow a+b-c=c\Rightarrow a+b=2c\)
tương tự như trên
ta có: b + c = 2a
a+c = 2b
\(\Rightarrow M=\frac{\left(a+b\right).\left(b+c\right).\left(c+a\right)}{abc}=\frac{2c.2a.2b}{abc}=2^3=8\)
T
10 tháng 8 2020
Ta có :
M = ( a + b + c - d ) + ( a + b - c + d ) + ( a - b + c + d ) + ( -a + b + c + d )
= a + b + c - d + a + b - c + d + a - b + c + d - a + b + c + d
= ( a + a + a - a ) + ( b + b - b + b ) + ( c - c + c + c ) + ( - d + d + d + d )
= 2a + 2b + 2c + 2d
= 2 . ( a + b + c + d )
Thay a = 1 , b = 10 , c = 100 và d = 1000 vào biểu thức M có :
M = 2 .( 1 + 10 + 100 + 1000 )
M = 2 . 1111
M = 2222
Vậy M = 2222 khi a = 1 , b = 10 , c = 100 và d = 1000 .
Học tốt
PN
10 tháng 8 2020
\(M=\left(a+b+c-d\right)+\left(a+b-c+d\right)+\left(a-b+c+d\right)+\left(-a+b+c+d\right)\)
\(=a+b+c-d+a+b-c+d+a-b+c+d-a+b+c+d\)
\(=\left(a+b+c+d\right).3-\left(a+b+c+d\right)=2\left(a+b+c+d\right)\)
\(=2\left(1+10+100+1000\right)=2.1111=2222\)
CM
17 tháng 10 2017
Đáp án đúng a=2; b=4 hoặc a=4 thì b=2. Sai ở chỗ tại sao a=1; b= 5
CM
1 tháng 9 2018
Đáp án đúng a=2; b=4 hoặc a=4 thì b=2. Sai ở chỗ tại sao a=1; b= 5
PT
0
4 tháng 2 2022
a: Ta có: \(\widehat{MAC}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AM//BC
Ta có: \(\widehat{NAB}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//BC
Ta có: AM//BC
AN//BC
mà AM,AN có điểm chung là A
nên N,A,M thẳng hàng
b: Đặt \(\widehat{B}=x;\widehat{C}=y\)
Theo đề, ta có:
\(\left\{{}\begin{matrix}x-y=10\\x+y=110\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=60\\y=50\end{matrix}\right.\)