Tìm m ∈ ( 0 ; 5 6 ) sao cho hình phẳng giới hạn bởi các đường y = x 3 3 + m x 2 - 2 x - 2 m - 1 3 , x=0, x=2, y=0 có diện tích bằng 4
A. m = 1 2
B. m = 2 3
C. m = 1 4
D. m = 3 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 10 2018
Đúng(0)
Những câu hỏi liên quan
XO
12 tháng 2 2023
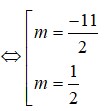
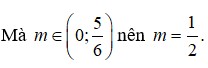
a) (*) m = 0 => x = \(\dfrac{7}{8}\) (loại)
(*) \(m\ne0\) Phương trình có nghiệm
\(\Delta=\left[2\left(m-4\right)\right]^2-4m\left(m+7\right)=-60m+64\ge0\Leftrightarrow m\le\dfrac{16}{15}\)
Hệ thức Viet kết hợp 4x1 + 3x2 = 1
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2=\dfrac{m+7}{m}\\x_1+x_2=\dfrac{8-2m}{m}\\x_1=2x_2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2=\dfrac{m+7}{m}\\x_1=\dfrac{16-4m}{3m}\\x_2=\dfrac{8-2m}{3m}\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{16-4m}{3m}.\dfrac{8-2m}{3m}=\dfrac{m+7}{m}\)
\(\Leftrightarrow2\left(8-2m\right)^2=9m\left(m+7\right)\)
\(\Leftrightarrow8m^2-64m+128=9m^2+63m\)
\(\Leftrightarrow m^2+127m-128=0\Leftrightarrow\left[{}\begin{matrix}m=1\\m=128\left(\text{loại}\right)\end{matrix}\right.\)<=> m = 1
26 tháng 11 2021
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
ĐKXĐ: \(x\ge0\)
\(\left(x^2-x-m\right)\sqrt{x}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-x-m=0\left(1\right)\end{matrix}\right.\)
Giả sử (1) có nghiệm thì theo Viet ta có \(x_1+x_2=1>0\Rightarrow\left(1\right)\) luôn có ít nhất 1 nghiệm dương nếu có nghiệm
Do đó:
a. Để pt có 1 nghiệm \(\Leftrightarrow\left(1\right)\) vô nghiệm
\(\Leftrightarrow\Delta=1+4m< 0\Leftrightarrow m< -\dfrac{1}{4}\)
b. Để pt có 2 nghiệm pb
TH1: (1) có 1 nghiệm dương và 1 nghiệm bằng 0
\(\Leftrightarrow m=0\)
TH2: (1) có 2 nghiệm trái dấu
\(\Leftrightarrow x_1x_2=-m< 0\Leftrightarrow m>0\)
\(\Rightarrow m\ge0\)
c. Để pt có 3 nghiệm pb \(\Leftrightarrow\) (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=1+4m>0\\x_1x_2=-m>0\\\end{matrix}\right.\) \(\Leftrightarrow-\dfrac{1}{4}< m< 0\)
HP
5 tháng 1 2021
1.
Yêu cầu bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}\Delta=25-12m>0\\x_1^2+x_2^2< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(x_1+x_2\right)^2-2x_1x_2< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(2m-3\right)^2-2\left(m^2-4\right)< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\2m^2-12m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \dfrac{25}{12}\)
HT
4 tháng 3 2021
\(a=-1< 0;\Delta=\left(2\sqrt{m}-1\right)^2+4\left(\sqrt{m}-m\right)=4m-4\sqrt{m}+1+4\sqrt{m}-4m=1>0\)
a/ \(f\left(x\right)\ge0\) vô nghiệm \(\Leftrightarrow f\left(x\right)< 0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(tm\right)\\\Delta< 0\left(voly\right)\end{matrix}\right.\)
Vậy ko tồn tại m để ....
b/ \(f\left(x\right)\ge0,\forall x\in\left[1;2\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left[{}\begin{matrix}1< x_1< x_2\\x_1< x_2< 2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-1.f\left(1\right)>0\\\dfrac{x_1+x_2}{2}-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}-1.f\left(2\right)>0\\\dfrac{x_1+x_2}{2}-2< 0\end{matrix}\right.\end{matrix}\right.\)
\(\left(1\right)\left\{{}\begin{matrix}-1+2\sqrt{m}-1-m+\sqrt{m}< 0\\\sqrt{m}-\dfrac{1}{2}-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-3\sqrt{m}+2>0\\\sqrt{m}>\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}0< m< 1\\m>2\end{matrix}\right.\\m>\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow m>\dfrac{9}{4}\)
\(\left(2\right)\left\{{}\begin{matrix}-4+4\sqrt{m}-2-m+\sqrt{m}< 0\\\sqrt{m}-\dfrac{1}{2}-2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-5\sqrt{m}+6>0\\\sqrt{m}< \dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}0< m< 2\\m>3\end{matrix}\right.\\0\le m< \dfrac{25}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}0< m< 2\\3< m< \dfrac{25}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{9}{4}\\0< m< 2\\3< m< \dfrac{25}{4}\end{matrix}\right.\)
9 tháng 11 2023
Ta có \(y'=-3x^2+6mx\)
Để hàm số đã cho nghịch biến trên \(ℝ\) thì
\(f\left(x\right)=-3x^2+6mx\le0,\forall x\inℝ\)
Thế thì \(\Delta'=9m^2-\left(-3\right).0\le0\) \(\Leftrightarrow m=0\)
Vậy để hàm số đã cho nghịch biến trên \(ℝ\) thì \(m=0\)
9 tháng 1
a: \(x^2+\left(2m+1\right)x+m^2-3=0\)
\(\text{Δ}=\left(2m+1\right)^2-4\left(m^2-3\right)\)
\(=4m^2+4m+1-4m^2+12=4m+13\)
Để phương trình có nghiệm kép thì 4m+13=0
=>\(m=-\dfrac{13}{4}\)
Thay m=-13/4 vào phương trình, ta được:
\(x^2+\left(2\cdot\dfrac{-13}{4}+1\right)x+\left(-\dfrac{13}{4}\right)^2-3=0\)
=>\(x^2-\dfrac{11}{2}x+\dfrac{121}{16}=0\)
=>\(\left(x-\dfrac{11}{4}\right)^2=0\)
=>x-11/4=0
=>x=11/4
b: TH1: m=2
Phương trình sẽ trở thành \(\left(2+1\right)x+2-3=0\)
=>3x-1=0
=>3x=1
=>\(x=\dfrac{1}{3}\)
=>Khi m=2 thì phương trình có nghiệm kép là x=1/3
TH2: m<>2
\(\text{Δ}=\left(m+1\right)^2-4\left(m-2\right)\left(m-3\right)\)
\(=m^2+2m+1-4\left(m^2-5m+6\right)\)
\(=m^2+2m+1-4m^2+20m-24\)
\(=-3m^2+22m-23\)
Để phương trình có nghiệm kép thì Δ=0
=>\(-3m^2+22m-23=0\)
=>\(m=\dfrac{11\pm2\sqrt{13}}{3}\)
*Khi \(m=\dfrac{11+2\sqrt{13}}{3}\) thì \(x_1+x_2=\dfrac{-m-1}{m-2}=\dfrac{2-2\sqrt{13}}{3}\)
=>\(x_1=x_2=\dfrac{1-\sqrt{13}}{3}\)
*Khi \(m=\dfrac{11-2\sqrt{13}}{3}\) thì \(x_1+x_2=\dfrac{-m-1}{m-2}=\dfrac{2+2\sqrt{13}}{3}\)
=>\(x_1=x_2=\dfrac{1+\sqrt{13}}{3}\)
c: TH1: m=0
Phương trình sẽ trở thành
\(0x^2-\left(1-2\cdot0\right)x+0=0\)
=>-x=0
=>x=0
=>Nhận
TH2: m<>0
\(\text{Δ}=\left(-1+2m\right)^2-4\cdot m\cdot m\)
\(=4m^2-4m+1-4m^2=-4m+1\)
Để phương trình có nghiệm kép thì -4m+1=0
=>-4m=-1
=>\(m=\dfrac{1}{4}\)
Khi m=1/4 thì \(x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left[-1+2m\right]}{m}=\dfrac{-2m+1}{m}\)
=>\(x_1+x_2=\dfrac{-2\cdot\dfrac{1}{4}+1}{\dfrac{1}{4}}=\dfrac{-\dfrac{1}{2}+1}{\dfrac{1}{4}}=\dfrac{1}{2}:\dfrac{1}{4}=2\)
=>\(x_1=x_2=\dfrac{2}{2}=1\)
19 tháng 11 2021
\(\Leftrightarrow\Delta=4\left(m-2\right)^2-4m\left(m-3\right)=0\\ \Leftrightarrow4m^2-16m+16-4m^2+12m=0\\ \Leftrightarrow16-4m=0\\ \Leftrightarrow m=4\)
Chọn B