Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng ∆ đi qua điểm A ( 2 ; - 1 ; 3 ) và vuông góc với mặt phẳng (Oxz) là.
A. x = 2 y = 1 - t z = 3
B. x = 2 y = 1 + t z = 3
C. x = 2 y = - 1 + t z = 3
D. x = 2 + t y = - 1 z = 3 + t
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có ![]() = (1, -2, -2)
= (1, -2, -2)
Phương trình đường thẳng AB đi qua B(2;-1;0) nhận véc-tơ ![]() làm véc-tơ chỉ phương nên có phương trình là:
làm véc-tơ chỉ phương nên có phương trình là:
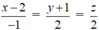

Chọn D.
Ta có (P) qua O(0;0;0) và nhận BA → = ( 1 ; 3 ; - 5 ) là một VTPT
⇒ ( P ) : x + 3 y - 5 z = 0 .

Đáp án D.
Ta có A B → = ( 1 ; - 5 ; 4 )
Đường thẳng AB có vecto chỉ phương A B → = ( 1 ; - 5 ; 4 ) nên loại đáp án A, B
Thay tọa độ A(1;2;-3) vào đáp án C được
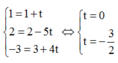
hay điểm A không thuộc đường thẳng ở đáp án C, còn lại đáp án D.

Chọn A.
∆ đi qua hai điểm A và B nên có vectơ chỉ phương A B → 2 ; 3 ; - 4
Vậy phương trình chính tắc của ∆ là x - 1 2 = y + 2 3 = z - 5 - 4

Đáp án B
Ta có M N → = 1 ; − 1 ; 1 nên đường thẳng MN có một vectơ chỉ phương là u M N → = 1 ; − 1 ; 1 . Mà đường thẳng MN đi qua điểm N 2 ; 1 ; 4 nên có phương trình tham số là x = 2 + t y = 1 − t z = 4 + t , t ∈ ℝ .
Chọn C.
Mặt phẳng (Oxz) có vectơ pháp tuyến j → 0 ; 1 ; 0
Vì ∆ vuông góc với mp(Oxz) nên ∆ có vectơ chỉ phương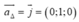
∆ đi qua điểm A(2;-1;3) và có vectơ chỉ phương a ∆ →
Vậy phương trình tham số của ∆ là x = 2 y = - 1 + t z = 3