Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017; 2017]để hàm số y = (m − 2)x + 2m đồng biến trên R.
A. 2014
B. 2016
C. Vô số
D. 2015
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
19 tháng 12 2021
Lời giải:
Để $(m^2-4)x=m(m-2)$ có nghiệm duy nhất thì $m^2-4\neq 0$
$\Leftrightarrow (m-2)(m+2)\neq 0$
$\Leftrightarrow m\neq \pm 2$
Mà $m$ nguyên và $m\in [-5;5]$ nên $m\in\left\{-5; -4; -3; -1; 0; 1;3;4;5\right\}$
CM
14 tháng 2 2017
Chọn D
Phương pháp:
Sử dụng: Hàm số y = ax+b đồng biến ⇔ a > 0, từ đó kết hợp điều kiện đề bài để tìm các giá trị của m.
Cách giải:
Hàm số y = (m-2)x + 2 đồng biến trên ℝ ⇔ m - 2 > 0 ⇔ m > 2
Mà 
=> có 2016 giá trị nguyên của m thỏa mãn đề bài.
CM
9 tháng 9 2017
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
CM
5 tháng 3 2019
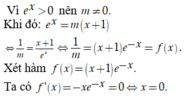
Dựa vào BBT, ta thấy phương trình có nghiệm duy nhất
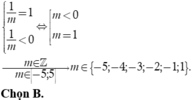
Ta có y = e x là hàm đồng biến trên ℝ và y = e x > 0 với mọi x ∈ ℝ có đồ thị (C)(xem hình 1).
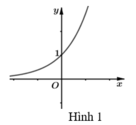
Do đó:
= Nếu m < 0 thì y = m(x+1) là hàm số nghịch biến trên ℝ , có đồ thị là một đường thẳng luôn qua điểm (-1;0) nên luôn cắt đồ thị (C): y = e x tại duy nhất một điểm.
= Nếu m = 0 phương trình vô nghiệm (do y = e x > 0).
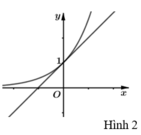
= Nếu m > 0 để phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng
là tiếp tuyến của (C) (như hình 2)
CM
11 tháng 3 2019
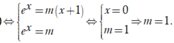
+) Phương trình ban đầu có nghiệm khi và chỉ khi phương trình bậc hai ẩn t có nghiệm dương.
Cách giải:
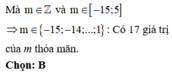
Đáp án D