cho hàm số y=x2-2(m+\(\frac{1}{m}\))x +m (m>0) xác định trên [ -1; 1] GTLN GTNN của hs trên [-1; 1 ] lần lượt là y1 y2 thỏa mãn y1-y2=8 khi đó m =
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 1 2021
Đặt y= f(x) = \(x^2-2\left(m+\dfrac{1}{m}\right)x+m\)
Hoành độ đỉnh của đồ thị hàm số x=\(m+\dfrac{1}{m}\ge2\) (BĐT co-si)
vì hệ số a =1>0 nên hàm số nghịch biến trên \(\left(-\infty;m+\dfrac{1}{m}\right)\)
Suy ra, hàm số nghịch biến trên \(\left[-1;1\right]\)
=> y1 = f(-1) = \(3m+\dfrac{2}{m}+1\)
y2 = f(1)=\(1-m-\dfrac{2}{m}\)
theo đề bài ta có : y1-y2=8 <=> \(3m+\dfrac{2}{m}+1-1+m+\dfrac{2}{m}=8\left(m>0\right)\)
<=> \(m^2-2m+1=0\)
<=> m=1
HN
0
CM
16 tháng 8 2019
Đáp án: D.
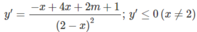
⇔ ∆ ′ = 2m + 5 ≤ 0
dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (- ∞ ; 2)
và (2; + ∞ ) khi m ≤ −5/2.
NT
0
CM
8 tháng 2 2019
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 
CM
13 tháng 7 2019
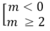
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
∆ ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 
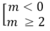
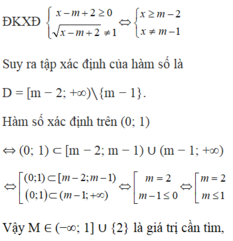
\(a=1>0\); \(-\frac{b}{2a}=m+\frac{1}{m}\ge2>1\)
\(\Rightarrow\) Hàm số đã cho nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_1=\max\limits_{\left[-1;1\right]}f\left(x\right)=f\left(-1\right)=3m+\frac{2}{m}+1\)
\(y_2=f\left(1\right)=-m-\frac{2}{m}+1\)
\(\Rightarrow y_1-y_2=4m+\frac{4}{m}=8\)
\(\Leftrightarrow m^2-2m+1=0\Rightarrow m=1\)