Cho hàm số sau y = tan2x – tanx + 2, x ∈ [ - π 4 ; π 4 ]. Chọn khẳng định đúng
A: max y = 3 3
B: max y = 4
C: min y = - 3
D: Tất cả sai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Đặt \(cos2x=t\Rightarrow t\in\left[-1;1\right]\)
Xét hàm \(y=f\left(t\right)=2t^2+2t-4\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{2}\in\left[-1;1\right]\)
\(f\left(-1\right)=-4\) ; \(f\left(-\dfrac{1}{2}\right)=-\dfrac{9}{2}\) ; \(f\left(1\right)=0\)
\(\Rightarrow y_{min}=-\dfrac{9}{2}\) khi \(t=-\dfrac{1}{2}\) hay \(cos2x=-\dfrac{1}{2}\)
\(y_{max}=0\) khi \(cos2x=1\)
b. Đặt \(tanx=t\Rightarrow t\in\left[-1;\sqrt{3}\right]\)
Xét hàm \(f\left(t\right)=t^2-2\sqrt{3}t-1\) trên \(\left[-1;\sqrt{3}\right]\)
\(-\dfrac{b}{2a}=\sqrt{3}\in\left[-1;\sqrt{3}\right]\)
\(f\left(-1\right)=2\sqrt{3}\) ; \(f\left(\sqrt{3}\right)=-4\)
\(y_{min}=-4\) khi \(x=\dfrac{\pi}{3}\) ; \(y_{max}=2\sqrt{3}\) khi \(x=-\dfrac{\pi}{4}\)

1:
a: ĐKXĐ: \(x< >\dfrac{\Omega}{2}+k\Omega\)
=>TXĐ: \(D=R\backslash\left\{\dfrac{\Omega}{2}+k\Omega\right\}\)
b: ĐKXĐ: \(x< >k\Omega\)
=>TXĐ: \(D=R\backslash\left\{k\Omega\right\}\)
c: ĐKXĐ: \(2x< >\dfrac{\Omega}{2}+k\Omega\)
=>\(x< >\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\)
TXĐ: \(D=R\backslash\left\{\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\right\}\)
d: ĐKXĐ: \(3x< >\Omega\cdot k\)
=>\(x< >\dfrac{k\Omega}{3}\)
TXĐ: \(D=R\backslash\left\{\dfrac{k\Omega}{3}\right\}\)
e: ĐKXĐ: \(x+\dfrac{\Omega}{3}< >\dfrac{\Omega}{2}+k\Omega\)
=>\(x< >\dfrac{\Omega}{6}+k\Omega\)
TXĐ: \(D=R\backslash\left\{\dfrac{\Omega}{6}+k\Omega\right\}\)
f: ĐKXĐ: \(x-\dfrac{\Omega}{6}< >\Omega\cdot k\)
=>\(x< >k\Omega+\dfrac{\Omega}{6}\)
TXĐ: \(D=R\backslash\left\{k\Omega+\dfrac{\Omega}{6}\right\}\)

+ Xét hàm số y= f(x) = cos3x
TXĐ: D =R
Với mọi x ∈ D , ta có: - x ∈ D và
f( -x) = cos( - 3x) = cos3x = f(x)
Do đó, y= cos 3x là hàm chẵn trên tập xác định của nó.
+ Xét hàm y= g(x)= sin(x2 + 1)
TXĐ: D= R
Với mọi x ∈ D , ta có: - x ∈ D và
g( -x)= sin[ (-x)2 +1]= sin( x2+1)= g(x)
Do đó: y= sin( x2 +1) là hàm chẵn trên R.
+ Xét hàm số y= h( x)= tan2x .
TXĐ: 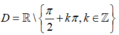
Với mọi x ∈ D , ta có: - x ∈ D và
h( -x)= tan2 (-x)= (- tanx)2 = tan2 x= h(x)
Do đó y= tan2x là hàm số chẵn trên D.
+ Xét hàm số y= t(x)= cotx.
TXĐ: ![]()
Với mọi x ∈ D , ta có: - x ∈ D và t(-x)= cot(-x) = - cotx = - t(x)
Do đó: y= cotx là hàm số lẻ trên D.
Vậy (1); (2); (3) là các hàm số chẵn
Đáp án C
Đáp án B