Giải phương trình chú thích(^ là mũ; /là chia )
(5^3-1/3^2-1 : 9^2-1/7^2-1 :13^2-1/11^2-1 : ... : 45^2-1/43^2-1 ) : 1/x -1=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
29 tháng 5 2017
Copy trên Wolframalpha nè:
Hãy thử như sau:- Sử dụng các cách diễn giải khác hoặc ký hiệu khác
- Nhập toàn bộ từ thay vì chữ viết tắt
- Tránh trộn các ký hiệu toán học và các ký hiệu khác
- Kiểm tra chính tả của bạn
- Cung cấp cho bạn đầu vào bằng tiếng Anh
- Wolfram | Alpha trả lời các câu hỏi cụ thể hơn là giải thích các chủ đề chungNhập "2 chén đường", chứ không phải "thông tin dinh dưỡng"
- Bạn chỉ có thể nhận được câu trả lời về sự thật khách quanHãy thử "ngọn núi cao nhất", không phải "bức tranh đẹp nhất"
- Chỉ có điều Wolfram | Alpha biết đếnHỏi "có bao nhiêu người ở Mauritania", chứ không phải "bao nhiêu quái vật ở Loch Ness"
- Chỉ có thông tin công khaiYêu cầu "GDP của Pháp", chứ không phải "điện thoại của Michael Jordan"
- Approximate forms
- More solutions
- Các mẫu gần đúng
- Giải pháp từng bước
DQ
4
YT
15 tháng 6 2018
\(4x^4-11x^2+6=0\)
\(\Leftrightarrow4x^4-8x^2-3x^2+6=0\)
\(\Leftrightarrow4x^2\left(x^2-2\right)-3\left(x^2-2\right)=0\)
\(\Leftrightarrow\left(x^2-2\right)\left(4x^2-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-2=0\\4x^2-3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\pm\sqrt{2}\\x=\pm\sqrt{\frac{3}{4}}\end{cases}}\)
\(S=\left\{\pm\sqrt{2};\pm\sqrt{\frac{3}{4}}\right\}\)
nếu có sai bn thông cảm nha
CM
1 tháng 8 2019
a) 16. 2 x + 4. 2 x = 5. 5 x + 3. 5 x
⇔ 20. 2 x = 8. 5 x ⇔ (2/5)x = ( 2 / 5 ) 1 ⇔ x = 1
b) 16. 7 x − 16. 5 2 x = 0
⇔ 7 x = 5 2 x ⇔ ( 7 / 25 ) x = ( 7 / 25 ) 0 ⇔ x = 0
c) Chia hai vế cho 12 x ( 12 x > 0), ta được:
4 ( 3 / 4 ) x + 1 − 3 ( 4 / 3 ) x = 0
Đặt t = ( 3 / 4 ) x (t > 0), ta có phương trình:
4t + 1 − 3/t = 0 ⇔ 4 t 2 + t − 3 = 0
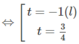
Do đó, ( 3 / 4 ) x = ( 3 / 4 ) 1 . Vậy x = 1.
d) Đặt t = 2 x (t > 0), ta có phương trình:
− t 3 + 2 t 2 + t – 2 = 0
⇔ (t − 1)(t + 1)(2 − t) = 0
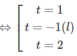
Do đó: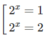 
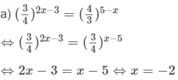
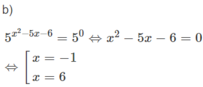
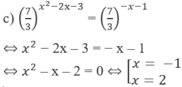
CM
2 tháng 3 2018
d) Hướng dẫn: Lấy logarit cơ số 2 cả hai vế
Phương trình đã cho có hai nghiệm phân biệt đều thỏa mãn điều kiện
15 tháng 6 2018
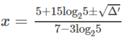
Đặt \(a=x^2\)
\(\Rightarrow4a^2-11a+6=0\)
ta có: \(\Delta=11^2-4.4.6=121-96=25>0\)
=> Phương trình có 2 nghiệm phân biệt: \(a1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{11+\sqrt{25}}{2.4}=\frac{16}{8}=2\Leftrightarrow x^2=2\Leftrightarrow x=\pm\sqrt{2}\)
\(a2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{11-\sqrt{25}}{2.4}=\frac{6}{8}=\frac{3}{4}\)\(\Leftrightarrow x^2=\frac{3}{4}\Leftrightarrow x=\pm\sqrt{\frac{3}{4}}\)
