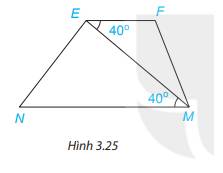
Quan sát Hình 3.25. Biết \(\widehat {MEF} = 40^\circ ;\widehat {EMN} = 40^\circ \). Em hãy giải thích tại sao EF // NM.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Các góc kề với \(\widehat {xOy}\) là: \(\widehat {yOz};\widehat {yOt}\)
b) Ta có:
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} + \widehat {zOt} = \widehat {xOt}\\ \Rightarrow 20^\circ + \widehat {zOt} + \widehat {zOt} = 90^\circ \\ \Rightarrow 2.\widehat {zOt} = 90^\circ - 20^\circ = 70^\circ \\ \Rightarrow \widehat {zOt} = 70^\circ :2 = 35^\circ \end{array}\)

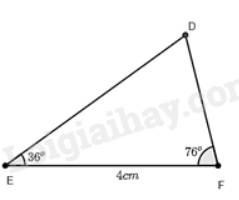
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.

a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)

a) Vì a,b cùng vuông góc với đường thẳng AB nên a // b
b) Vì \(\widehat {{B_1}} = \widehat {{C_2}}( = 40^\circ )\). Mà 2 góc này ở vị trí so le trong nên b // c ( Dấu hiệu nhận biết 2 đường thẳng song song)
c) Vì a // b, b //c nên a // c

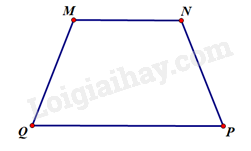
a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)
Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)
b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.
Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)

Vì \(\widehat {xAz} = \widehat {yBz}( = 50^\circ )\)
Mà hai góc này ở vị trí đồng vị nên Ax//By (Dấu hiệu nhận biết hai đường thẳng song song)

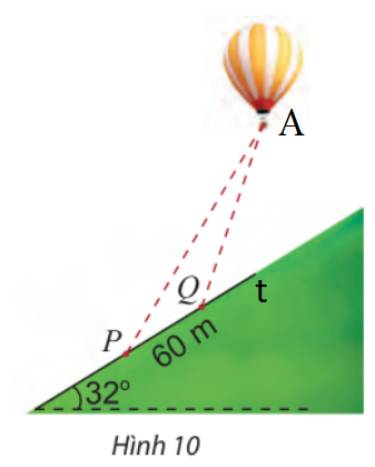
Gọi A là vị trí của khinh khí cầu, Pt là đường sườn đồi như hình.
Ta có:
Tại P, góc nâng của khinh khí cầu là \({62^ \circ }\)\( \Rightarrow \widehat P = {62^ \circ } - {32^ \circ } = {30^ \circ }\)
Tại Q, góc nâng của khinh khí cầu là \({70^ \circ }\)\( \Rightarrow \widehat {AQt} = {70^ \circ } - {32^ \circ } = {38^ \circ }\)
\( \Rightarrow \widehat {AQP} = {180^ \circ } - {38^ \circ } = {142^ \circ }\) và \(\widehat A = {180^ \circ } - {142^ \circ } - {30^ \circ } = {8^ \circ }\)
Áp dụng định lí sin trong tam giác APQ, ta có:
\(\begin{array}{l}\frac{{PQ}}{{\sin A}} = \frac{{QA}}{{\sin P}}\\ \Rightarrow QA = \sin P.\frac{{PQ}}{{\sin A}} = \sin {30^ \circ }.\frac{{60}}{{\sin {8^ \circ }}} \approx 215,56\;(m)\end{array}\)
Vậy khoảng cách từ Q đến khinh khí cầu là 215,56 m.

a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)

Vì Ax // Dy, mà AD \( \bot \) Ax nên AD \( \bot \) Dy. Do đó, \(\widehat{ADC}=90^0\)
Vì Ax // Dy nên \(\widehat {ABC} = \widehat {BCy}\) ( 2 góc so le trong), mà \(\widehat {BCy} = 50^\circ \Rightarrow \widehat {ABC} = 50^\circ \)
Vậy \(\widehat{ADC}=90^0; \widehat {ABC} = 50^\circ \)
Vì \(\widehat {FEM} = \widehat {EMN}( = 40^\circ )\)
Mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) EF // NM ( Dấu hiệu nhận biết hai đường thẳng song song)