vẽ đồ thị hàm số \(y=\cot x\) rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng \(\left(-\pi;\pi\right)\) là nghiệm của mỗi phương trình sau :
1) \(\cot x=\frac{\sqrt{3}}{3}\) ; 2) \(\cot x=1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
6 tháng 9 2016
a) Trên hình là đô thị hàm số y = tanx , đường y = - 1 , y = 0 ( chính là trục x'Ox ) . ( thiếu hình vẽ )
Các điểm \(\left(-\frac{\pi}{4};-1\right);\left(\frac{3\pi}{4};-1\right)...\) là các điểm có hoành độ là nghiệm của phương trình tanx = - 1 . Các điểm \(\left(-\pi;0\right),\left(0;0\right),\left(\pi;0\right)\) , là các điểm có hoành độ là nghiệm của phương trình tanx = 0
b) Học sinh tự vẽ đô thị hàm số y = cotx và chỉ ra các điểm có hoành độ là nghiệm của phương cotx = \(\frac{\sqrt{3}}{3};cotx=1\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Do hoành độ giao điểm nằm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) nên: \(\tan x = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Do hoành độ giao điểm nằm trên khoảng \(\left( {0;\pi } \right)\) nên: \(\cot x = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng\(\left( {0;\pi } \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) \(x=-1\Rightarrow y=0\\ x=0\Rightarrow y=3\\ x=1\Rightarrow y=4\\ x=2\Rightarrow y=3\\ x=3\Rightarrow y=0\)
Lần lượt là: A(-1;0), B(0;3), I(1;4), C(2;3), D(3;0)
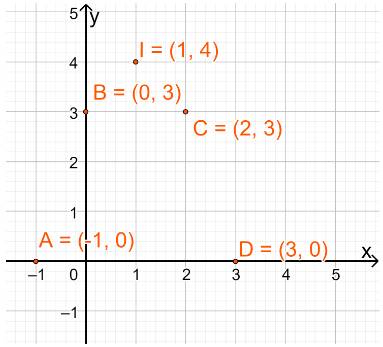
b) Vẽ đồ thị:
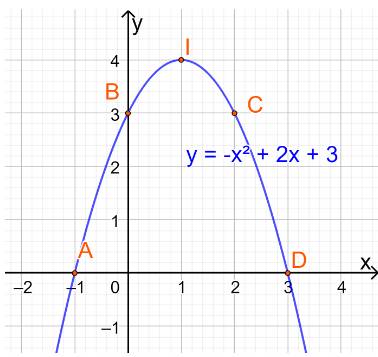
c) Điểm cao nhất là điểm I(1;4)
Phương trình trục đối xứng là đường thẳng x=1.
Đồ thị hàm số đó quay bề lõm xuống dưới.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a)
+) Thay tọa độ \(\left( { - 1; - 2} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\( - 2 = - 2.{\left( { - 1} \right)^2}\)(Đúng)
=> \(\left( { - 1; - 2} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
+) Thay tọa độ \(\left( {0;0} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\(0 = - {2.0^2}\)(Đúng)
=> \(\left( {0;0} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
+) Thay tọa độ \(\left( {0;1} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\(1 = - {2.0^2} \Leftrightarrow 1 = 0\)(Vô lí)
=> \(\left( {0;1} \right)\) không thuộc đồ thị hàm số \(y = - 2{x^2}\).
+) Thay tọa độ \(\left( {2021;1} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\(1 = - {2.2021^2}\)(Vô lí)
=> \(\left( {2021;1} \right)\) không thuộc đồ thị hàm số \(y = - 2{x^2}\).
b)
+) Thay \(x = - 2\) vào hàm số \(y = - 2{x^2}\) ta được:
\(y = - 2.{\left( { - 2} \right)^2} = - 8\)
+) Thay \(x = 3\) vào hàm số \(y = - 2{x^2}\) ta được:
\(y = - {2.3^2} = - 18\)
+) Thay \(x = 10\) vào hàm số \(y = - 2{x^2}\) ta được:
\(y = - 2.{\left( {10} \right)^2} = - 200\)
c) Thay \(y = - 18\) vào hàm số \(y = - 2{x^2}\) ta được:
\( - 18 = - 2{x^2} \Leftrightarrow {x^2} = 9 \Leftrightarrow x = \pm 3\)
Vậy các điểm có tọa độ (3;-18) và (-3;-18) thuộc đồ thị hàm số có tung độ bằng -18.
29 tháng 12 2020
b) Vì A(xA;yA) có tung độ bằng 6 nên yA=6
Thay y=6 vào hàm số y=3x, ta được:
\(3\cdot x=6\)
hay x=2
Vậy: A(2;6)
c) Gọi điểm có tung độ và hoành độ bằng nhau trên đồ thị hàm số y=3x là B(xB;yB)
nên xB=yB
Thay x=y vào hàm số y=3x, ta được:
y=3y
\(\Leftrightarrow y=0\)
Vậy: Điểm trên đồ thị hàm số y=3x có tung độ và hoành độ bằng nhau có tọa độ là (0;0)