Cho phương trình ẩn x;
(m-1)x+7=0 .Tìm m để pt vô nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Để PT là PT bậc nhất 1 ẩn thì:
$m^2-m+1\neq 0$
$\Leftrightarrow (m-\frac{1}{2})^2+\frac{3}{4}>0$
Điều này luôn đúng với mọi $m\in\mathbb{R}$ do $(m-\frac{1}{2})^2+\frac{3}{4}\geq 0+\frac{3}{4}>0$ với mọi $m\in\mathbb{R}$
Vậy có vô số số thực $m$ thỏa mãn điều kiện đề.

Để phương trình đã cho là phương trình bậc nhất một ẩn thì m - 2 ≠ 0
⇔ m ≠ 2

a: Phương trình có dạng ax+b=0 khi a<>0 được gọi là phương trình bậc nhất một ẩn
Phương trình 2x-5=2x+3 là phương trình bậc nhất một ẩn
c: Hai phương trình tương đương là hai phương trình có cùng tập nghiệm

\(m^2x=m\cdot\left(x+2\right)-2\)
\(\Leftrightarrow x\left(m^2-m\right)-2m+2=0\)
*Nếu m=1 <=> m^2 - m = 0 \(\Leftrightarrow-2.1+2=0\left(Đ\right)\)
=> Với m =1 thì pt thỏa mãn với mọi x thuộc R
*Nếu \(m\ne1\Leftrightarrow x=\frac{2m-2}{m^2-m}\)
=> Với \(m\ne1\text{ thì }x=\frac{2m-2}{m^2-m}\)
Vậy ....

a,để PT trở thành bậc nhất một ản thì m-3\(\ne0\Leftrightarrow m\ne3\)
thay x=2 vào biểu thức ta có m=-143(tm)

Khi a = 1, ta có phương trình:
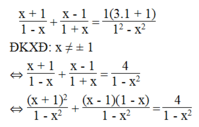
⇔ x + 1 2 + (x – 1)(1 – x) = 4
⇔ x 2 + 2x + 1 + x – x 2 – 1 + x = 4
⇔ 4x = 4 ⇔ x = 1 (loại)
Vậy phương trình vô nghiệm.

Khi a = - 3, ta có phương trình:
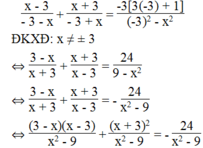
⇔ (3 – x)(x – 3) + x + 3 2 = -24
⇔ 3x – 9 – x 2 + 3x + x 2 + 6x + 9 = -24 ⇔ 12x = - 24
⇔ x = -2 (thỏa mãn)
Vậy phương trình có nghiệm x = -2

Khi a = 0, ta có phương trình:
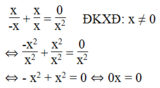
Phương trình nghiệm đúng với mọi giá trị của x ≠ 0
Vậy phương trình có nghiệm x ∈ R / x ≠ 0.