a) Vẽ (P): \(y=-2x^2\);(D):\(y=x-3\)
b) Tìm tọa độ giao điểm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
0
HM
0
24 tháng 11 2022
Bài 3:
b: \(tan\left(a_1\right)=-2\)
nên \(a_1\simeq117^0\)
\(tan\left(a_2\right)=-1\)
nên a2=135 độ
\(tan\left(a3\right)=-0,5\)
nên a3=153 độ
Bài 2:
b: \(tan\left(a1\right)=0,5\)
nên a1=27 độ
\(tan\left(a2\right)=1\)
nên a2=45 độ
\(tan\left(a3\right)=2\)
nên a3=64 độ
TP
0
2
23 tháng 5 2023
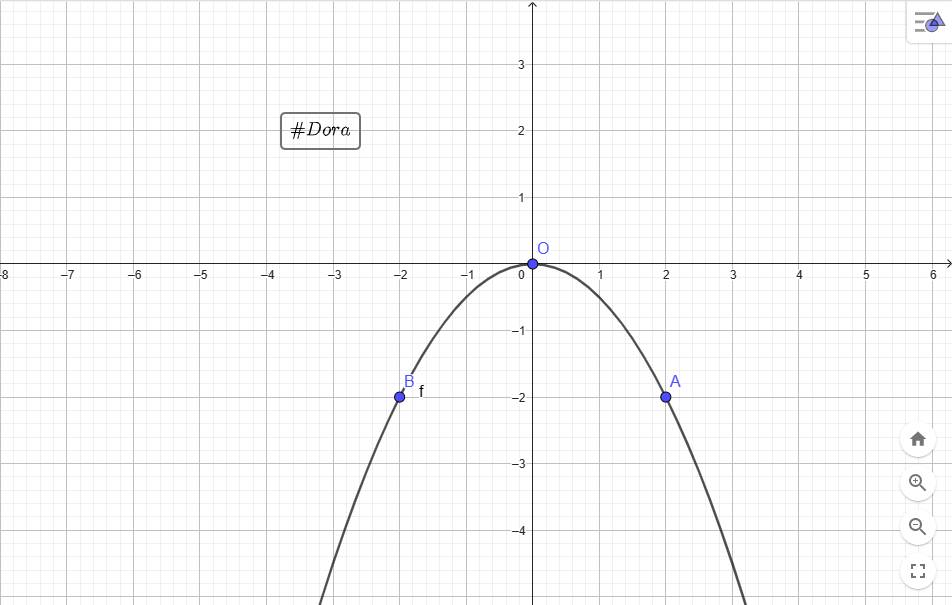
`a)O(0;0), A(2;-2), B(-2;-2) in (P)`
`b)` Gọi `(d_1): y=ax+b`
Vì `(d_1) //// (d)=>a=2` và `b ne 1`
Thay `a=1`, ptr hoành độ của `(P)` và `(d_1)` là:
`-1/2x^2=x+b`
`<=>x^2+2x+2b=0` `(1)`
`(P)` tiếp xúc với `(d_1)<=>` Ptr `(1)` có nghiệm kép
`=>\Delta'=0`
`<=>1-2b=0`
`<=>b=1/2` (t/m)
`=>` Ptr `(d_1): y=x+1/2`
b) PTHĐGĐ của (P) và (d)
\(-2x^2=x-3\\ \Leftrightarrow2x^2+x-3=0\\ \Leftrightarrow\left(x-1\right)\left(2x+3\right)=0\\ \left[{}\begin{matrix}x=1\\x=\dfrac{-3}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}y=-2\\y=-\dfrac{9}{2}\end{matrix}\right.\)
Vậy (d) cắt (P) tại 2 điểm A(1,-2) ,B(\(-\dfrac{3}{2},-\dfrac{9}{2}\))
Vẽ hình ra dùm mình đi.