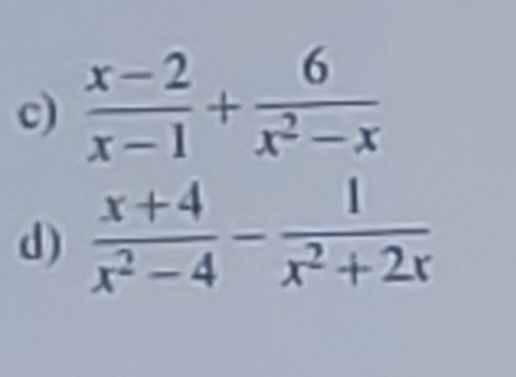 thực hiện phép tính phân thức đại số
thực hiện phép tính phân thức đại số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


9\(x^2\) - 4 = (2\(x\) - 1).(2 - 3\(x\))
9\(x^2\) - 4 = 4\(x\) - 6\(x^2\) - 2 + 3\(x\)
9\(x^2\) - 4 - 4\(x\) + 6\(x^2\) + 2 - 3\(x\) = 0
(9\(x^2\) + 6\(x^2\)) - (4\(x\) + 3\(x\)) - (4 - 2) = 0
15\(x^2\) - 7\(x\) - 2 = 0
15\(x^2\) - 10\(x\) + 3\(x\) - 2 = 0
5\(x\)(3\(x\) - 2) + (3\(x\) - 2) = 0
(3\(x\) - 2)(5\(x\) + 1) = 0
\(\left[{}\begin{matrix}3x-2=0\\5x+1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy\(x\) \(\in\) {- \(\dfrac{1}{5}\); \(\dfrac{2}{3}\)}
\(9x^2-4=\left(2x-1\right)\left(2-3x\right)\\ \Leftrightarrow\left(3x-2\right)\left(3x+2\right)=\left(2x-1\right)\left(2-3x\right)\\ \Leftrightarrow\left(3x-2\right)\left(3x+2\right)-\left(2x-1\right)\left(2-3x\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(3x+2\right)+\left(2x-1\right)\left(3x-2\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(3x+2+2x-1\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(5x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}3x-2=0\\5x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{1}{5}\end{matrix}\right.\)

B = \(\dfrac{x^2+x-5x-5}{x^2-10x+25}\) (đk: \(x\ne5\))
B = \(\dfrac{x\left(x+1\right)-5\left(x+1\right)}{\left(x-5\right)^2}\)
B = \(\dfrac{\left(x+1\right).\left(x-5\right)}{\left(x-5\right)^2}\)
B = \(\dfrac{x+1}{x-5}\)

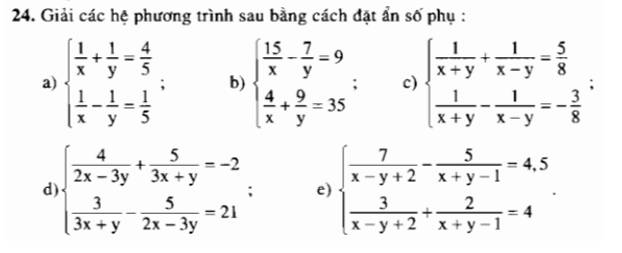
a:
ĐKXĐ: \(x\ne0;y\ne0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\)
Hệ phương trình sẽ trở thành \(\left\{{}\begin{matrix}a+b=\dfrac{4}{5}\\a-b=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=1\\a-b=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=a-\dfrac{1}{5}=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{2}\\\dfrac{1}{y}=\dfrac{3}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{10}{3}\end{matrix}\right.\left(nhận\right)\)
b: ĐKXĐ: \(x\ne0;y\ne0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}15a-7b=9\\4a+9b=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}60a-28b=36\\60a+135b=140\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-163b=-104\\4a+9b=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{104}{163}\\a=\dfrac{4769}{652}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{4769}{652}\\\dfrac{1}{y}=\dfrac{104}{163}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{652}{4769}\\y=\dfrac{163}{104}\end{matrix}\right.\)(nhận)
c: ĐKXĐ: \(x\ne\pm y\)
Đặt \(\dfrac{1}{x+y}=a;\dfrac{1}{x-y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}a+b=\dfrac{5}{8}\\a-b=-\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=\dfrac{5}{8}-\dfrac{3}{8}=\dfrac{2}{8}=\dfrac{1}{4}\\a+b=\dfrac{5}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{1}{4}\\b=\dfrac{5}{8}-\dfrac{1}{4}=\dfrac{3}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x+y}=\dfrac{1}{4}\\\dfrac{1}{x-y}=\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=4\\x-y=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=4+\dfrac{8}{3}=\dfrac{20}{3}\\x+y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{10}{3}\\y=4-x=4-\dfrac{10}{3}=\dfrac{2}{3}\end{matrix}\right.\left(nhận\right)\)
d: ĐKXĐ: \(y\ne-3x;y\ne\dfrac{2}{3}x\)
Đặt \(\dfrac{1}{2x-3y}=a;\dfrac{1}{3x+y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}4a+5b=-2\\-5a+3b=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}20a+25b=-10\\-20a+12b=84\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}37b=84-10=74\\4a+5b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2\\a=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{2x-3y}=-3\\\dfrac{1}{3x+y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\3x+y=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\9x+3y=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=-\dfrac{1}{3}+\dfrac{3}{2}=\dfrac{7}{6}\\y=\dfrac{1}{2}-3x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{7}{66}\\y=\dfrac{1}{2}-3\cdot\dfrac{7}{66}=\dfrac{1}{2}-\dfrac{7}{22}=\dfrac{4}{22}=\dfrac{2}{11}\end{matrix}\right.\)
e: ĐKXĐ:\(x\ne y-2;x\ne-y+1\)
Đặt x-y+2=a; x+y-1=b
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}\dfrac{7}{a}-\dfrac{5}{b}=4,5\\\dfrac{3}{a}+\dfrac{2}{b}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{14}{a}-\dfrac{10}{b}=9\\\dfrac{15}{a}+\dfrac{10}{b}=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{29}{a}=29\\\dfrac{3}{a}+\dfrac{2}{b}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=1\\\dfrac{2}{b}=4-\dfrac{3}{a}=4-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y+2=1\\x+y-1=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-1\\x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)(nhận)

Nếu chia 15 dư 6 thì chắc chắn sẽ chia hết cho 3
Nếu chia 9 dư 1 thì chắc chắn sẽ không bao giờ chia hết cho 3
Do đó, hai điều này đối nghịch nhau
Từ đó suy ra, không có số tự nhiên nào chia 15 dư 6 và chia 9 dư 1
Giả sử tồn tại một số a chia cho 15 dư 6 và chia 9 dư 1 khi đó ta có:
\(\left\{{}\begin{matrix}a=15k+6\left(k\in N\right)\\15k+6-1⋮9\end{matrix}\right.\) ⇒ 15k + 6 - 1 ⋮ 3 ⇒ 15k + 5 ⋮ 3 ⇒ 3.(5k + 1) + 2 ⋮ 3
⇒ 2 ⋮ 3 (vô lí) Điều giả sử là sai.
Vậy không có số tự nhiên nào mà chia cho 15 dư 6 và chia 9 dư 1

a: Xét ΔABC có BM là phân giác
nên \(\dfrac{AM}{MC}=\dfrac{BA}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
=>\(\dfrac{AM}{3}=\dfrac{MC}{5}\)
mà AM+MC=AC=6cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{3}=\dfrac{MC}{5}=\dfrac{AM+MC}{3+5}=\dfrac{6}{8}=\dfrac{3}{4}\)
=>\(AM=3\cdot\dfrac{3}{4}=\dfrac{9}{4}\left(cm\right)\)
b: Xét ΔEBC có GQ//BC
nên \(\dfrac{EG}{EB}=\dfrac{EQ}{EC}\)
Xét ΔMBC có QI//BC
nên \(\dfrac{CI}{CM}=\dfrac{BQ}{BM}\)
Ta có: \(\widehat{ABM}=\widehat{MBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\widehat{ECB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACE}=\widehat{MBC}=\widehat{ECB}\)
Xét ΔQBC có \(\widehat{QBC}=\widehat{QCB}\)
nên ΔQBC cân tại Q
=>QB=QC
Xét ΔAMB và ΔAEC có
\(\widehat{ABM}=\widehat{ACE}\)
AB=AC
\(\widehat{BAM}\) chung
Do đó: ΔAMB=ΔAEC
=>MB=EC
mà MB=MQ+QB
và EC=EQ+QC
và QB=QC
nên MQ=EQ
\(\dfrac{EG}{EB}+\dfrac{CI}{CM}=\dfrac{EQ}{EC}+\dfrac{BQ}{BM}=1-\dfrac{CQ}{CE}+\dfrac{BQ}{BM}\)
\(=1-\dfrac{BQ}{BM}+\dfrac{BQ}{BM}=1\)

\((z-3)^2-(x-2y)^2\\=[(z-3)-(x-2y)][(z-3)+(x-2y)]\\=(z-3-x+2y)(z-3+x-2y)\)
\(\left(z-3\right)^2-\left(x-2y\right)^2\)
\(=\left[\left(z-3\right)-\left(x-2y\right)\right]\left[\left(z-3\right)+\left(x-2y\right)\right]\)
\(=\left(z-3-x+2y\right)\left(z-3+x-2y\right)\)

\(\frac{x-1}{1999}+\frac{x-2}{1998}=\frac{x-3}{1997}+\frac{x-4}{1996}\\\Leftrightarrow \left(\frac{x-1}{1999}-1\right) +\left(\frac{x-2}{1998}-1\right)=\left(\frac{x-3}{1997}-1\right)+\left(\frac{x-4}{1996}-1\right)\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}=\frac{x-2000}{1997}+\frac{x-2000}{1996}\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}-\frac{x-2000}{1997}-\frac{x-2000}{1996}=0\\ \Leftrightarrow (x-2000)\left(\frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\right)=0\\\Leftrightarrow x-2000=0\left(\text{vì } \frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\ne0\right)\\\Leftrightarrow x=2000\)
Vậy phương trình đã cho có 1 nghiệm duy nhất là \(x=2000\).

ĐỐI VỚI BÀI TOÁN LẬP PHƯƠNG TRÌNH VỀ QUÃNG ĐƯỜNG VẬN TỐC THỜI GIAN THÌ NÊN LẬP BẢNG ĐỂ GIẢI DỄ DÀNG HƠN
| vận tốc | quãng đường | thời gian | |
| A - B | x + 10 | 4(x + 10) | 4 |
| B - A | x - 10 | 5(x - 10) | 5 |
vì vận tốc của dòng nước là 10km/h nên:
vận tốc cano đi từ A đến B là: x + 10 (km/h)
vận tốc cano đi từ B đến A là: x - 10 (km/h)
quãng đường cano đi từ A đến B là: 4(x + 10) (km)
quãng đường cano đu từ B đến A là: 5(x - 10) (km)
theo đề ta có phương trình:
4(x + 10) = 5(x - 10)
4x + 40 = 5x - 50
4x - 5x = -40 - 50
-x = -90
x = 90
quãng đường AB dài là: 4(90+10) = 400 (km)
VẬY QUÃNG ĐƯỜNG AB DÀI 400KM
Cùng quãng sông nên vận tốc và thời gian tỉ lệ nghịch
Tỉ số thời gian đi xuôi so với đi ngược là : \(\dfrac{4}{5}\)
=> Tỉ số vận đi xuôi so với đi ngược là : \(\dfrac{5}{4}\)
Ta có sơ đồ:
Vận tốc đi xuôi :|------|------|------|------|------|
Vận tốc đi ngược :|------|------|------|------|
Hiệu vận tốc đi xuôi với đi ngược là:
10 x 2 = 20 (km/giờ)
=> Vận tốc đi xuôi dòng của ca nô là:
20 : (5 - 4) x 5 = 100 (km/giờ)
=> Khoảng cách từ A đến B là:
100 x 4 = 400 (km)
Đ/s: 400 km

Tự vẽ hình nhé.
a) Theo bài ra ABCD là HCN
=> AD=BC (1) ; AD//BC
Do AD//BC => ADB=DBC (2 góc so le trong) hay ADN=CBM (2)
Ta có AN vuông góc với BD => AND=ANB=90
CM vuông góc với BD => CMD=CMB=90
Xét tam giác AND và tam giác CMB có
AND=CMB=90
AD=BC ( theo (1) )
ADN = CBM ( theo (2) )
=> tam giác AND= tam giác CMB (cạnh huyền-góc nhọn)
=> ND = MB (2 cạnh tương ứng) (dpcm)
b) Do AN vuông góc với BD và CM vuông góc với BD
=>AN//CM (mối quan hệ từ vuông góc đến song song)
Lại có: tam giác AND= tam giác CMB (cạnh huyền-góc nhọn)
=> AN = CM (2 cạnh tương ứng)
Xét tứ giác ANCM có AN=CM và AN//CM
=> tứ giác ANCM là hình bình hành.
c) Lại thấy AN//CM => KN // CM
Xét tứ giác KCMN có KN=CM và KN // CM
=> tứ giác KCMN là hình bình hành
=> KC // MN
=> KC//BD
Xét tứ giác DKCB có KC//BD => tứ giác DKCB là hình thang.
d) Do K là điểm đối xứng với A qua N
=>NA=NK
=> N là trung điểm của AK.
=>PN là đường trung tuyến của tam giác AKP.
Mặt khác KC//MN => CP//MB => BMP= MPC (2 góc so le trong)
Mà AMN=BMP (2 góc đồng vị)
Từ đó suy ra AMN=MPC
Vì ANM=90 nên tam giác ANM vuông tại N
=> NAM +AMN = 90
Vì MC vuông góc với BD mà BD//CP
=> MC vuông góc với CP (mqh..)
=> MCP = 90 => tam giác MCP vuông tại C => CMP+MPC=90
Do đó NAM + AMN = CMP + MPC = 90
Mà AMN=MPC
=> NAM = CMP
Xét tam giác ANM và tam giác MCP có
NAM = CMP (theo cmt)
AN=CM (từ phần b)
ANM=MCP(=90)
=> tam giác ANM = tam giác MCP (cạnh huyền-cạnh góc vuông)
=> AN=MP( 2 cạnh tương ứng)
và MN =CP ( 2 cạnh tương ứng)
Vì MN=CK và MN=CP
=> CK=CP
=> C là trung điểm của PK
=>AC là đường trung tuyến của tam giác AKP.
Do AM=MP => M là trung điểm của AP
=>KM là đường trung tuyến của tam giác AKP.
Xét tam giác AKP có PN là đường trung tuyến của tam giác AKP.
AC là đường trung tuyến của tam giác AKP.
KM là đường trung tuyến của tam giác AKP.
Từ đó suy ra PN, AC, KM đồng quy tại trọn tâm của tam giác AKP
Vậy..
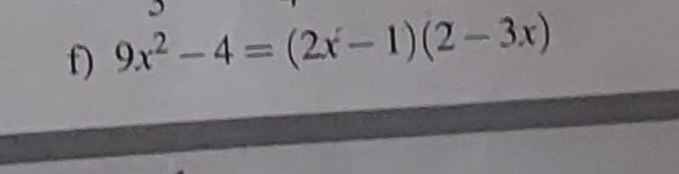
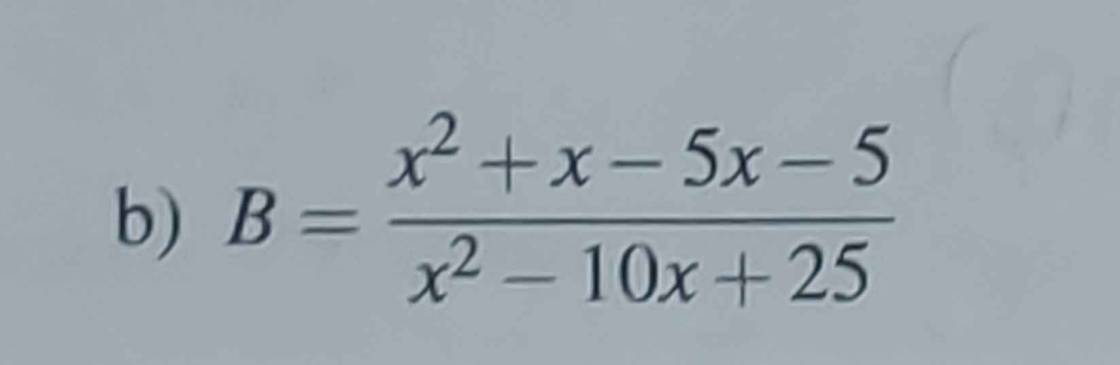



c) \(\dfrac{x-2}{x-1}+\dfrac{6}{x^2-x}\)
\(=\dfrac{x\left(x-2\right)}{x\left(x-1\right)}+\dfrac{6}{x\left(x-1\right)}\)
\(=\dfrac{x^2-2x+6}{x\left(x-1\right)}\)
\(=\dfrac{x^2-2x+6}{x^2-x}\)
d) \(\dfrac{x+1}{x^2-4}-\dfrac{1}{x^2+2x}\)
\(=\dfrac{x+1}{\left(x+2\right)\left(x-2\right)}-\dfrac{1}{x\left(x+2\right)}\)
\(=\dfrac{x\left(x+1\right)}{x\left(x+2\right)\left(x-2\right)}-\dfrac{x-2}{x\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+x-x+2}{x\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+2}{x\left(x^2-4\right)}\)
\(=\dfrac{x^2+2}{x^3-4x}\)