Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TUYÊN TRUYỀN LOẠI CON TRẦN LÊ KIM MAI RA KHỎI OLM MỚI TUẦN TRC ĐIỂM NÓ LÀ 500 THÔI, NHG TUẦN NẦY NÓ LÊN TỚI GẦN 2000, ĐÃ LÊN NHG BỊ OLM TRỪ ĐIỂM DO SỰ TUYÊN TRUYỀN CỦA E Cảm ơn OLM đã trừ điểm con súc vật TRẦN LÊ KIM MAI ,link của nó https://olm.vn/thanhvien/kimmai123az, e rất ghi nhận sự tiến bộ về sự công bằng của olm.Nhưng vẫn còn nhìu cây mà con chó này copy nek, mong olm xét ạ https://olm.vn/hoi-dap/detail/228356929591.html////////https://olm.vn/hoi-dap/detail/228472453946.html/////https://olm.vn/hoi-dap/detail/228437567447.html//////////https://olm.vn/hoi-dap/detail/228435268921.html Vô trangh cá nhân của e sẽ thấy đc những câu trả lời \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\"siêu hay\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\" của con chóhttps://olm.vn/thanhvien/kimmai123az Nó ms lớp 7 mà lamfg đc tón 9, nó tôi bt , là một người ko đàng hoàng , siêu nói tục của OLM, 1 ví dụ điển hình cho con cái nhà ko có giáo dục, nó chửi e là thèm cặc, lồn, bướm lồn, cave, các a chị vô trang cá nhân của e , vô thống kê hỏi đáp sẽ thấy nhg lời thô tục của nó. Em đăng ko để kiếm điểm nhg để vạch trần bộ mặt của con đó, e ko cần điêm làm j, nhg nếu mn thấy đúng thì k cx đc. E ko bốc phốt con chó ấy , đang chỉ ra nhg đứa dốt nát, đi copy bài

a: Ta có: ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔACF có
O,E lần lượt là trung điểm của AC,AF
=>OE là đường trung bình của ΔACF
=>OE//CF và \(OE=\dfrac{1}{2}CF\)
Xét tứ giác OEFC có OE//FC
nên OEFC là hình thang
ta có: OE//CF
I\(\in\)CF
Do đó: OE//CI
Ta có: OE=CF/2
CI=CF/2
Do đó: OE=CI
Xét tứ giác OEIC có
OE//IC
OE=IC
Do đó: OEIC là hình bình hành
b: Xét tứ giác CHFK có \(\widehat{CHF}=\widehat{CKF}=\widehat{HCK}=90^0\)
nên CHFK là hình chữ nhật

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành
B A C D E K

I A B C E H D L G F K
a) Do I đối xứng với D qua H nên HI = HD.
Xét tứ giác BDEI có HI = HD; HB = HE nên BDEI là hình bình hành.
Lại có \(\widehat{EDB}=90^o\) nên BDEI là hình chữ nhật.
b) Do BDEI là hình chữ nhật nên IE // BD và IE = BD.
Vậy thì ta cũng có ngay IE // DL và IE = DL
Suy ra tứ giác IDLE là hình bình hành (dấu hiệu nhận biết)
c) Xét tam giác EBL có ED là đường cao đồng thời trung tuyến. Vậy tam giác EBL cân tại E hay \(\widehat{EBL}=\widehat{ELB}\)
Do tam giác ABC cân tại A nên \(\widehat{EBL}=\widehat{ACB}\) , suy ra \(\widehat{ACB}=\widehat{ELB}\)
Chúng lại ở vị trí đồng vị nên EL // GC.
Theo câu b, IDLE là hình bình hành nên IE // DL và ID // EL , vậy thì ID // GC
Xét tứ giác IGCD có: IG // DC; ID // GC nên IGDC là hình bình hành.
d) Ta có EG // BC nên tam giác AEG cân tại A hay AE = AG
Xét tam giác vuông FEG có AE = AG nên \(\widehat{AEG}=\widehat{AGE}\Rightarrow\widehat{AFE}=\widehat{AEF}\Rightarrow AE=AF\)
Vậy thì A là trung điểm EF.
Theo đề bài thì DFKC là hình chữ nhật nên FK song song và bằng DC
Lại có IGCD là hình bình hành nên IG song song và bằng DC.
Vậy thì FK song song và bằng IG hay FKGI là hình bình hành.
Suy ra FG và IK cắt nhau tại trung điểm mỗi đường.
A là trung điểm FG nên A là trung điểm IK. Vậy I, A, K thẳng hàng.

a: Xét tứ giác ACED có
AD//CE
AD=CE
Do đó: ACED là hình bình hành
b: Xét ΔIBA vuông tại B và ΔICK vuông tại C có
IB=IC
góc AIB=góc CIK
Do đo: ΔIBA=ΔICK
=>AB=CK
=>CK=CD
=>C là trung điểm của KD
Xét tứ giác DBKE có
DK cắt BE tại trung điểm của mỗi đường
DK vuông góc với BE
Do đó:DBKE là hình thoi

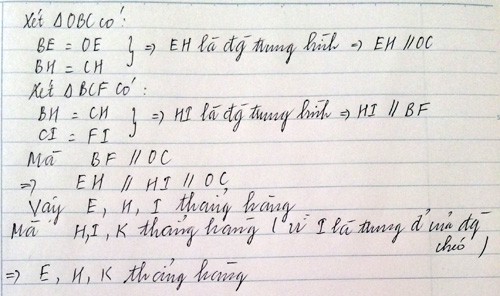

Hình tự vẽ nha.
a)Xét tứ giác ACED có : I là trung điểm AE (E đối xứng A qua I)
I là trung điểm DC (GT)
⇒ AD cắt CD tại trung điểm mỗi đường
⇒ACED là h bình hành (dấu hiệu nhận biết)
Vậy ....(đpcm)
b)Vì ABCD là h chữ nhật(GT) nên OD=OC và AD=BC(tính chất)
mà AD=CE (ACED là h bình hành)
nên CE=BC
Xét △BED có:HC là đường trung bình
( CE=BC, H là trung điểm DE)
⇒HC // BD ( định lí)
Xét tứ giác DOCHcó: DO//HC ( DB//HC, O ∈ DB)
DH//OC (ACED là h bình hành)
⇒DOCH là h bình hành ( dấu hiệu nhận biết)
Xét △DOI và △ COI có DI=IC( I là trung điểm CD)
OI chung
OD=OC (cmt)
⇒△DOI = △ COI(c.c.c)
⇒DO =OC (2 cạnh tương ứng)
Xét h bình hành DOCH (cmt) có DO=OC (cmt)
⇒DOCH là hình thoi( dấu hiệu nhận biết)
Vậy ...(đpcm)
Bạn tham khảo thôi nha, mình không chắc lắm