NQ
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KT
17 tháng 7 2018
d) mk chỉnh lại đề
\(8xy^2-5xyz-24y+15z\)
\(=xy\left(8y-5z\right)-3\left(8y-5z\right)\)
\(=\left(8y-5z\right)\left(xy-3\right)\)
e) \(x^4-x^3-x+1=\left(x-1\right)^2\left(x^2+x+1\right)\)
f) \(x^4+x^2y^2+y^4=\left(x^2-xy+y^2\right)\left(x^2+xy-y^2\right)\)
g) \(x^3+3x-4=\left(x-1\right)\left(x^2+x+4\right)\)
h) \(x^3-3x^2+2=\left(x-1\right)\left(x^2-2x-2\right)\)
i) \(2x^3+x^2-4x-12=\left(x-2\right)\left(2x^2+5x+6\right)\)
k) \(25x^2\left(x-5\right)-x+y=\left(1-5x\right)\left(1+5x\right)\left(y-x\right)\)
1 tháng 9 2018
Cái này chưa học bt làm mấy câu
b. x^2 + 2x - 3
= x^2 + 3x - x - 3
= x ( x - 1 ) + 3 ( x - 1 )
= ( x + 3 ) ( x - 1 )
TN
1 tháng 9 2018
\(4x^2-3x-4\)
\(=\left(2x\right)^2-2.2x.\frac{3}{4}+\frac{9}{16}-\frac{73}{16}\)
\(=\left(2x-\frac{3}{4}\right)^2-\frac{73}{16}\)
\(=\left(2x-\frac{3}{4}\right)^2-\left(\frac{\sqrt{73}}{4}\right)^2\)
\(=\left(2x-\frac{3}{4}-\frac{\sqrt{73}}{4}\right)\left(2x-\frac{3}{4}+\frac{\sqrt{73}}{4}\right)\)
\(=\left(2x-\frac{3+\sqrt{73}}{4}\right)\left(2x+\frac{-3+\sqrt{73}}{4}\right)\)
\(x^2+2x-3\)
\(=x^2-x+3x-3\)
\(=x\left(x-1\right)+3\left(x-1\right)\)
\(=\)\(\left(x+3\right)\left(x-1\right)\)
\(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\) \(\left(1\right)\)
đặt \(x^2+5x+5=t\)
\(\left(1\right)\)\(=\) \(\left(t-1\right)\left(t+1\right)-24\)
\(=t^2-1-24\)
\(=t^2-25\)
\(=\left(t-5\right)\left(t+5\right)\)
hay \(\left(1\right)=\left(x^2+5x+5-5\right)\left(x^2+5x+5+5\right)\)
\(=\left(x^2+5x\right)\left(x^2+5x+10\right)\)
\(=x\left(x+5\right)\left(x^2+5x+10\right)\)
học tốt
KC
2
21 tháng 8 2021
Ta có: \(A=2\left(x+y\right)^4-3\left(x+y\right)^2-5\)
\(=2\left(x+y\right)^4-5\left(x+y\right)^2+2\left(x+y\right)^2-5\)
\(=\left(x+y\right)^2\left[2\left(x+y\right)^2-5\right]+\left[2\left(x+y\right)^2-5\right]\)
\(=\left[2\left(x+y\right)^2-5\right]\left[\left(x+y\right)^2+1\right]\)
VT
1
YN
27 tháng 10 2021
\(\left(x+1\right).\left(x+2\right).\left(x+3\right).\left(x+4\right)-24\)
\(=[\left(x+1\right).\left(x+4\right)].[\left(x+2\right).\left(x+3\right)]-24\)
\(=\left(x^2+4x+x+4\right).\left(x^2+3x+2x+6\right)-24\)
\(=\left(x^2+5x+4\right).\left(x^2+5x+6\right)-24\)
Ta đặt \(n=x^2+5x+4\)
Lúc này biểu thức trở thành \(n.\left(n+2\right)-24\)
\(=n^2+2n-24\)
\(=n^2+2n+1-25\)
\(=\left(n+1\right)^2-5^2\)
\(=\left(n+1-5\right).\left(n+1+5\right)\)
\(=\left(n-4\right).\left(n+6\right)\)
\(=\left(x^2+5x+4-4\right).\left(x^2+5x+4+6\right)\)
\(=\left(x^2+5x\right).\left(x^2+5x+10\right)\)
C
1
1 tháng 11 2020
M = x9 - x7 + x6 - x5 - x4 + x3 - x2 + 1
= ( x9 - x7 ) + ( x6 - x4 ) - ( x5 - x3 ) - ( x2 - 1 )
= x7( x2 - 1 ) + x4( x2 - 1 ) - x3( x2 - 1 ) - ( x2 - 1 )
= ( x2 - 1 )( x7 + x4 - x3 - 1 )
= ( x - 1 )( x + 1 )[ x4( x3 + 1 ) - ( x3 + 1 ) ]
= ( x - 1 )( x + 1 )( x3 + 1 )( x4 - 1 )
= ( x - 1 )( x + 1 )( x + 1 )( x2 - x + 1 )( x2 - 1 )( x2 + 1 )
= ( x + 1 )2( x - 1 )( x2 - x + 1 )( x - 1 )( x + 1 )( x2 + 1 )
= ( x + 1 )3( x - 1 )2( x2 + 1 )( x2 - x + 1 )
TN
8
2 tháng 8 2016
\(x^4+x^3+x^2-1\)
\(=x^3\left(x+1\right)+\left(x+1\right)\left(x-1\right)\)
\(=\left(x+1\right)\left(x^3+\left(x-1\right)\right)\)
Ủng hộ nha ^ _ ^
AL
2 tháng 8 2016
\(x^4+x^3+x^2-1\)
\(=x^2\left(x^2-1\right)+x^2-1\)
\(=\left(x^2+1\right)\left(x^2-1\right)\)
20 tháng 5 2018
a) x2 + 6x + 9 = x2 + 2 . x . 3 + 32 = (x + 3)2
b) 10x – 25 – x2 = -(-10x + 25 +x2) = -(25 – 10x + x2)
= -(52 – 2 . 5 . x – x2) = -(5 – x)2
c) 8x3 - 1/8 = (2x)3 – (1/2)3 = (2x - 1/2)[(2x)2 + 2x . 12 + (1/2)2]
= (2x - 1/2)(4x2 + x + 1/4)
d)1/25x2 – 64y2 = (1/5x)2(1/5x)2- (8y)2 = (1/5x + 8y)(1/5x - 8y)
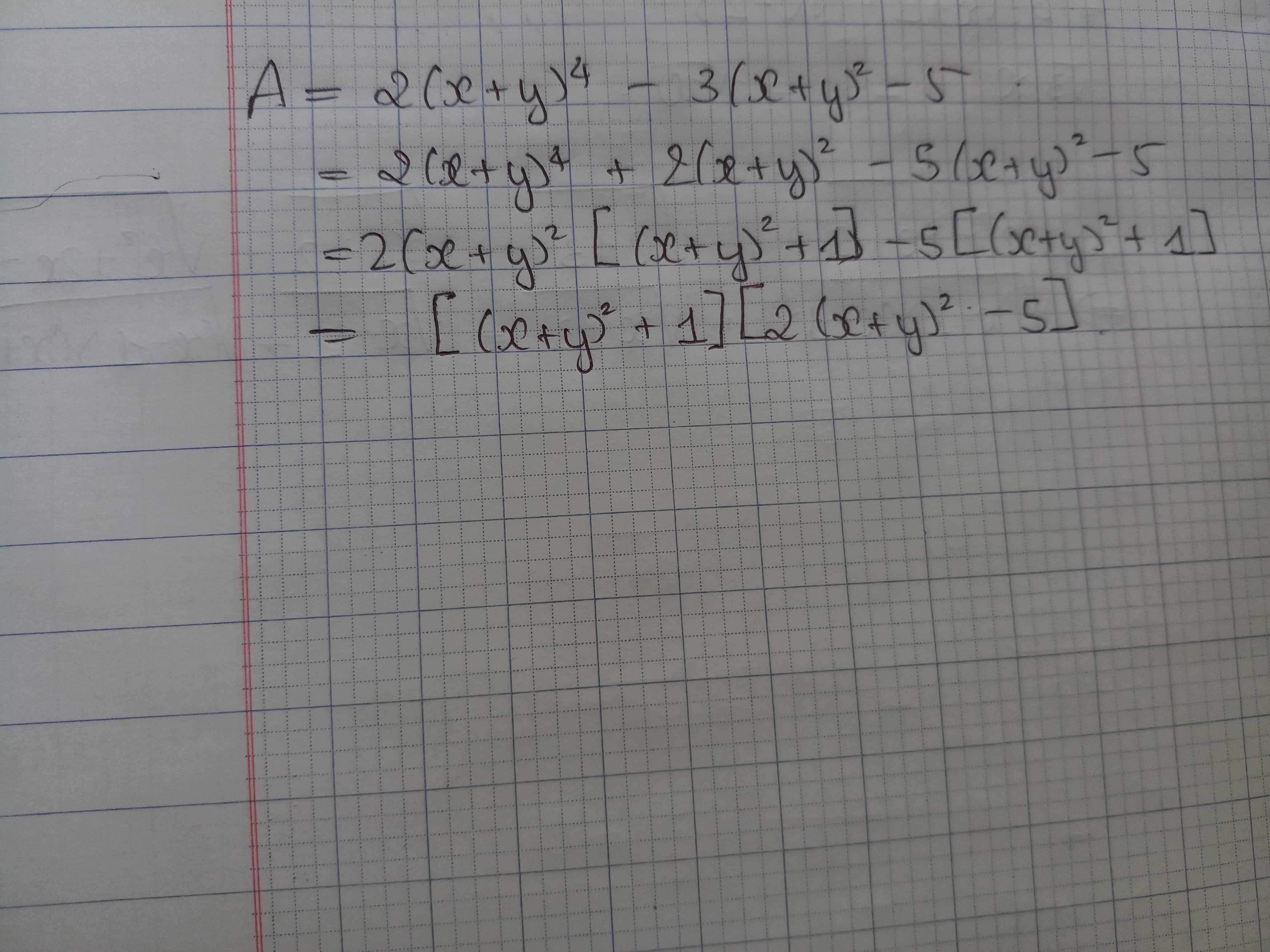
(x-1)(x-3)(x+2)(x+4)+21
\(=\left(x-1\right)\left(x+2\right)\left(x-3\right)\left(x+4\right)+21\)
\(=\left(x^2+x-2\right)\left(x^2+x-12\right)+21\)
\(=\left(x^2+x\right)^2-14\left(x^2+x\right)+24+21\)
\(=\left(x^2+x\right)^2-14\left(x^2+x\right)+45\)
\(=\left(x^2+x-5\right)\left(x^2+x-9\right)\)
Chúng ta có biểu thức:
(x−1)(x−3)(x+2)(x+4)+21(x-1)(x-3)(x+2)(x+4) + 21Bước 1: Tính (x−1)(x−3)=x2−4x+3(x-1)(x-3) = x^2 - 4x + 3 và (x+2)(x+4)=x2+6x+8(x+2)(x+4) = x^2 + 6x + 8.
Bước 2: Nhân hai kết quả lại:
(x2−4x+3)(x2+6x+8)=x4+2x3−13x2−14x+24(x^2 - 4x + 3)(x^2 + 6x + 8) = x^4 + 2x^3 - 13x^2 - 14x + 24Bước 3: Thêm 21 vào:
x4+2x3−13x2−14x+24+21=x4+2x3−13x2−14x+45x^4 + 2x^3 - 13x^2 - 14x + 24 + 21 = x^4 + 2x^3 - 13x^2 - 14x + 45Vậy, biểu thức đã phân tích là:
(x−1)(x−3)(x+2)(x+4)+21=x4+2x3−13x2−14x+45