Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

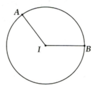
a, A I B ^ = 120 0 là góc tâm của (O; R) nên sđ A B ⏜ = 120 0
Áp dụng công thức tính độ dài cung tròn l = πRn 180 với R = 2cm; n 0 = 120 0
Độ dài cung nhỏ AB là: l = π . 2 . 120 180 = 4 π 3 cm
b, Diện tích hình quạt tròn giới hạn bởi cung nhỏ AB và hai bán kính IA, IB là phần tô màu xám
Áp dụng công thức: S = πR 2 n 360 với R = 2cm; n 0 = 120 0
Tính được S = 4 π 3 c m 2

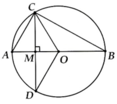
a, AC = 4cm => BC = 4 3 cm
=> R = 4cm => C = 8πcm, S = 16π c m 2
b, ∆AOC đều => A O C ^ = 60 0
=> C O D ^ = 120 0 => l C A D ⏜ = π . 4 . 120 180 = 8 π 3 cm
=> S = 8 π 3 . 4 2 = 16 π 3 c m 2

Từ O kẻ đg thg vg góc vs AB tại H
=> AH=BH=AB/2 = R căn 3 /2
Theo hệ thức lượng trong tam giác AHO vuông ở H ta có
SIN góc AOH = R căn 3 /2 : R
= căn 3/2 = 60
=> Góc AOB = 2 góc AOH= 2*60 =120
SĐ AB nhỏ =120
SĐ AB lớn = 360 - sđ AB nhỏ = 360 -120 = 240

Bài toán này liên quan đến hình học và tính toán trên đường tròn. Để giải bài toán này, chúng ta cần sử dụng các công thức hình học cơ bản.
a) Để tính khoảng cách từ điểm O đến đường AB, ta có thể sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
b) Để tính số đo cung nhỏ AB, ta cần sử dụng công thức tính độ dài cung trên đường tròn.
c) Để tính diện tích hình bán nguyệt giới hạn bởi dây cung AB và cung nhỏ AB, ta có thể sử dụng công thức tính diện tích hình tròn và hình tam giác.
d) Để tính IA và IB, ta có thể sử dụng định lý cosin trong tam giác vuông và các công thức hình học khác.