Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

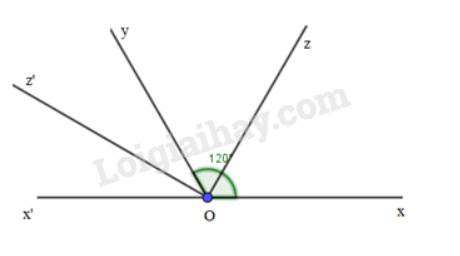
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau

Ta có: Oz là tia phân giác của \(\widehat{xOy}\) (gt)
\(\Rightarrow\widehat{xOz}=\widehat{yOz}\)
Vì \(Oz\perp Oz'\) (gt) nên: \(\widehat{yOz}+\widehat{yOz'}=90^o\)
Lại có: \(\widehat{xOz}+\widehat{yOz}+\widehat{yOz'}+\widehat{x'Oz'}=180^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}=180^o-\left(\widehat{yOz}+\widehat{yOz'}\right)\)
\(=180^o-90^o=90^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}=\widehat{yOz}+\widehat{yOz'}=90^o\)
Mà \(\widehat{xOz}=\widehat{yOz}\) (cmt)
\(\Rightarrow\widehat{x'Oz'}=\widehat{yOz'}\)
`=>` Tia Oz' là tia phân giác của \(\widehat{x'Oy}\) (đpcm)

a: góc x'Oy=180-140=40 độ
góc x'Oz=40/2=20 độ=góc yOz
góc xOz=180-20=160 độ
góc xOt=góc tOz=160/2=80 độ
b: góc xOt'=góc x'Ot=180 độ-góc xOt=100 độ
góc yOt'=góc x'Ot'+góc x'Oy=40+góc xOt
=40 độ+80 độ=120 độ
a)_Vì xoy+yox' = 180 độ(2 góc kb)
Có: yox= 140 đọ
⇒yox' = 180 độ - 140 độ = 40độ
Mà oz là tia phan giác yox'
⇒yoz=x'oz= 1/2yox' = 1/2.4= 20 độ
⇒zoy= 20 độ
⇒zox= 20 độ
_ Vì oy là tia phân giác xoy
⇒xot=yot=1/2xoy=1/2.140 độ= 70 độ
⇒xot = 70 độ
_ Vì xot + tox' = 180 độ(2 góc kề bù)
⇒tox'= 180 độ - 70 độ
tox' = 110 độ

1) Ta có: Oz nằm giữa tia Ox và Oy
\(\Rightarrow\widehat{xOz}=\widehat{xOy}-\widehat{yOz}=120^0-30^0=90^0\)
=> Oz⊥Ox
2) Ta có: Ox' là tia đối của tia Ox
\(\Rightarrow\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-120^0=60^0\)(2 góc kề bù)
Ta có: Ox' là tia đối của tia Ox, Oy' là tia đối của tia Oy
\(\widehat{\Rightarrow x'Oy'}=\widehat{xOy}=120^0\)(2 góc đối đỉnh)
1: Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOz}< \widehat{yOx}\)
nên tia Oz nằm giữa hai tia Ox và Oy
Suy ra: \(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{xOz}=90^0\)
hay Ox\(\perp\)Oz

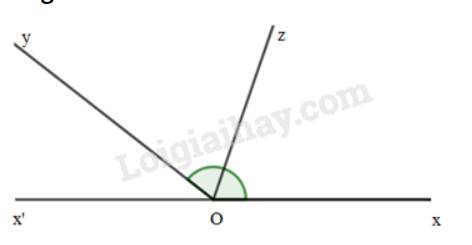
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.142^\circ = 71^\circ \)
Mà \(\widehat {x'Oz}\) và \(\widehat {xOz}\) là 2 góc kề bù nên \(\widehat {xOz} + \widehat {x'Oz} = 180^\circ \Rightarrow 71^\circ + \widehat {x'Oz} = 180^\circ \Rightarrow \widehat {x'Oz} = 180^\circ - 71^\circ = 109^\circ \)
Vậy \(\widehat {x'Oz} = 109^\circ \)
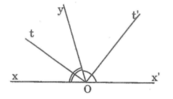
Ta có: \(\widehat{zOy}=\dfrac{1}{2}.\widehat{xOy}=\dfrac{1}{2}.120\text{°}=60\text{°}\)
\(\widehat{z'Oy}=\dfrac{1}{2}.\widehat{x'Oy}=\dfrac{1}{2}.\left(180\text{°}-\widehat{xOy}\right)=\dfrac{1}{2}.\left(180\text{°}-120\text{°}\right)=\dfrac{1}{2}.60\text{°}=30\text{°}\)
\(\widehat{zOz'}=\widehat{zOy}+\widehat{z'Oy}=60\text{°}+30\text{°}=90\text{°}\)