K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

PA
15 tháng 11 2016
AM = MB = AB/2 (M là trung điểm của AB)
BN = NC = BC/2 (N là trung điểm của BC)
CK = KD = CD/2 (K là trung điểm của CD)
mà AB = BC = CD (ABCD là hình vuông)
=> AM = MB = BN = NC = CK = KD
Xét tam giác BMC và tam giác CND có:
MB = NC (chứng minh trên)
MBC = NCD (= 900)
BC = CD (ABCD là hình vuông)
=> Tam giác BMC = Tam giác CND (c.g.c)
=> BMC = CND (2 góc tương ứng)
mà BMC + BCM = 900 (tam giác BMC vuông tại B)
=> CND + BCM = 900
=> CEN = 900 (CND + BCM + CEN = 1800)
=> CM _I_ DN
mà AH _I_ DN
=> AH // CM (1)
AM // CK
AM = CK (chứng minh trên)
=> AMCK là hình bình hành
=> AK // CM (2)
Từ (1) và (2)
=> \(AH\equiv AK\)
=> A, H, K thẳng hàng
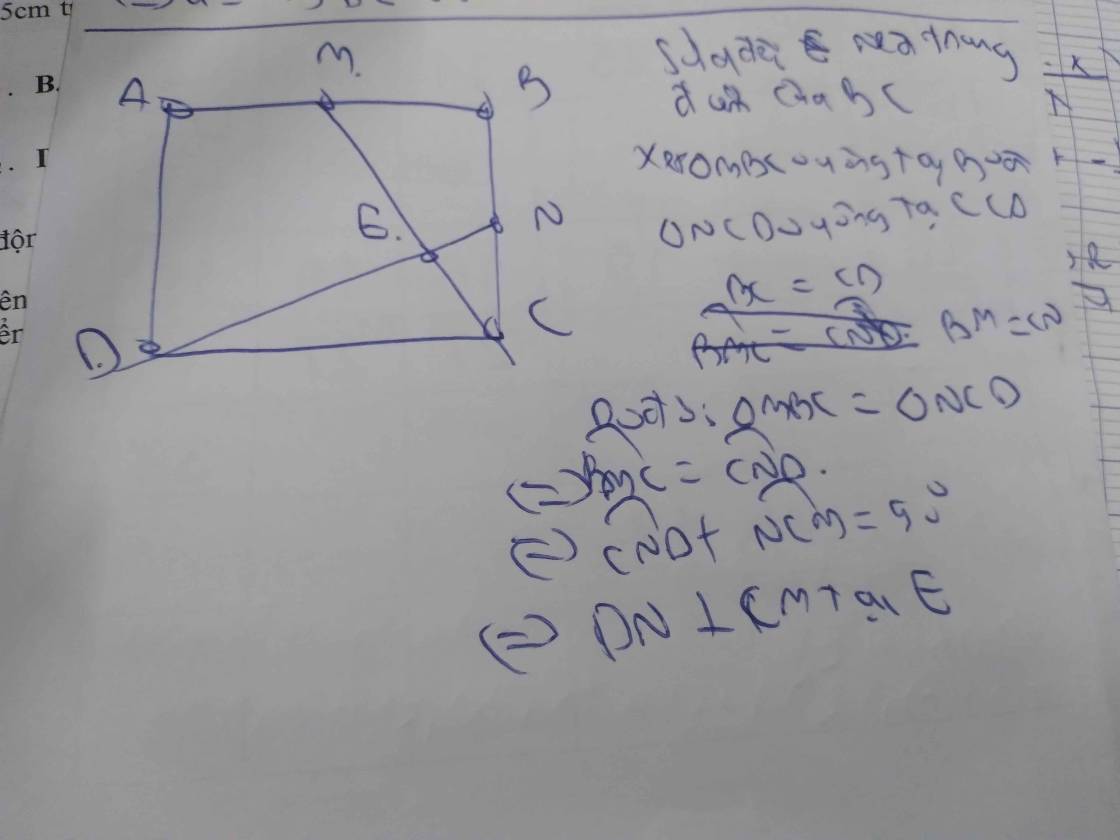
a) Vì tứ giác ABCD là hình vuông
nên \(\left\{{}\begin{matrix}AB=BC=CD=DA\\\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=\widehat{DAB}=90^{\circ}\end{matrix}\right.\) (t/c)
Mà: \(\left\{{}\begin{matrix}MA=MB=\dfrac{AB}{2}\\NB=NC=\dfrac{BC}{2}\end{matrix}\right.\) (do M, N lần lượt là trung điểm của AB, BC)
Do đó: \(MA=MB=NB=NC\)
Xét \(\Delta BCM\) và \(\Delta CDN\) có: \(\left\{{}\begin{matrix}MB=NC\left(cmt\right)\\\widehat{MBC}=\widehat{NCD}\left(=90^{\circ}\right)\\BC=CD\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta BCM=\Delta CDN\left(c.g.c\right)\)
\(\Rightarrow\widehat{BCM}=\widehat{CDN}\) (hai góc tương ứng)
Mà: \(\widehat{BCM}+\widehat{MCD}=\widehat{BCD}=90^{\circ}\) (hai góc kề phụ)
nên \(\widehat{CDN}+\widehat{MCD}=90^{\circ}\)
hay \(\widehat{CDH}+\widehat{HCD}=90^{\circ}\) (vì \(CM\cap DN=\left\{H\right\}\))
\(\Rightarrow\widehat{CHD}=90^{\circ}\Rightarrow CM\perp DN\) (đpcm)
b)
+, Gọi F là trung điểm của CD, G là giao điểm của AF với DH.
Xét \(\Delta DHC\) vuông tại H có: F là trung điểm của cạnh huyền CD
\(\Rightarrow HF=\dfrac{1}{2}CD=FD=FC\) (đli)
\(\Rightarrow F\) nằm trên đường trung trực của đoạn \(HD\) (1)
Vì F là trung điểm CD nên \(FC=FD=\dfrac{CD}{2}\)
Mà \(CD=AB;AM=BM=\dfrac{AB}{2}\left(cmt\right)\)
Do đó: \(FC=AM\)
Lại có: \(AB//CD\) (vì ABCD là hình vuông)
\(\Rightarrow AM//FC\) (vì \(M\in AB;F\in CD\))
Xét tứ giác AMCF có: \(\begin{cases} AM=FC(cmt)\\ AM//FC(cmt) \end{cases} \)
\(\Rightarrow\) Tứ giác AMCF là hình bình hành (t/c)
\(\Rightarrow AF//CM\) (t/c) \(\Rightarrow GF//HC\) (vì \(G\in AF;H\in CM\))
Xét \(\Delta DHC\) có: \(\begin{cases} F\text{ là trung điểm của CD }(cmt)\\ FG//HC\text{ }(cmt) \end{cases} \)
\(\Rightarrow G\) là trung điểm của DH (đli) (2)
Từ (1), (2) \(\Rightarrow FG\) là đường trung trực của đoạn DH
Mà \(A\in FG\Rightarrow\) A nằm trên đường trung trực của đoạn DH
\(\Rightarrow AD=AH\) (t/c) (*)
+, CMTT, ta cũng có: \(EH=EC\) (**)
Từ (*) và (**) \(\Rightarrow AD+EC=AH+EH=AE\) (vì \(H\in AE\)) (đpcm)
$Toru$
cái này chịu luôn nha