NN
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
Đoàn Đức Hà
Giáo viên
18 tháng 3 2022
Ta có: \(\frac{2022}{2021^2+k}\le\frac{2022}{2021^2}\) (với \(k\)là số tự nhiên bất kì)
Ta có:
\(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(\le\frac{2022}{2021^2}+\frac{2022}{2021^2}+...+\frac{2022}{2021^2}=\frac{2022}{2021^2}.2021=\frac{2022}{2021}\)
Ta có: \(\frac{2022}{2021^2+k}>\frac{2022}{2021^2+2021}=\frac{2022}{2021.2022}=\frac{1}{2021}\)với \(k\)tự nhiên, \(k< 2021\))
Suy ra \(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(>\frac{1}{2021}+\frac{1}{2021}+...+\frac{1}{2021}=\frac{2021}{2021}=1\)
Suy ra \(1< A\le\frac{2022}{2021}\)do đó \(A\)không phải là số tự nhiên.
LT
24 tháng 4 2022
Ta có: 202220212+k≤202220212202220212+k≤202220212 (với kklà số tự nhiên bất kì)
Ta có:
A=202220212+1+202220212+2+...+202220212+2021A=202220212+1+202220212+2+...+202220212+2021
≤202220212+202220212+...+202220212=202220212.2021=20222021≤202220212+202220212+...+202220212=202220212.2021=20222021
Ta có: 202220212+k>202220212+2021=20222021.2022=12021202220212+k>202220212+2021=20222021.2022=12021với kktự nhiên, k<2021k<2021)
Suy ra A=202220212+1+202220212+2+...+202220212+2021A=202220212+1+202220212+2+...+202220212+2021
>12021+12021+...+12021=20212021=1>12021+12021+...+12021=20212021=1
Suy ra 1<A≤202220211<A≤20222021do đó AAkhông phải là số tự nhiên.
DD
Đoàn Đức Hà
Giáo viên
18 tháng 3 2022
Ta có: \(\frac{2022}{2021^2+k}\le\frac{2022}{2021^2}\) (với \(k\)là số tự nhiên bất kì)
Ta có:
\(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(\le\frac{2022}{2021^2}+\frac{2022}{2021^2}+...+\frac{2022}{2021^2}=\frac{2022}{2021^2}.2021=\frac{2022}{2021}\)
Ta có: \(\frac{2022}{2021^2+k}>\frac{2022}{2021^2+2021}=\frac{2022}{2021.2022}=\frac{1}{2021}\)với \(k\)tự nhiên, \(k< 2021\))
Suy ra \(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(>\frac{1}{2021}+\frac{1}{2021}+...+\frac{1}{2021}=\frac{2021}{2021}=1\)
Suy ra \(1< A\le\frac{2022}{2021}\)do đó \(A\)không phải là số tự nhiên.
DD
Đoàn Đức Hà
Giáo viên
18 tháng 3 2022
Ta có: \(\frac{2022}{2021^2+k}\le\frac{2022}{2021^2}\) (với \(k\)là số tự nhiên bất kì)
Ta có:
\(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(\le\frac{2022}{2021^2}+\frac{2022}{2021^2}+...+\frac{2022}{2021^2}=\frac{2022}{2021^2}.2021=\frac{2022}{2021}\)
Ta có: \(\frac{2022}{2021^2+k}>\frac{2022}{2021^2+2021}=\frac{2022}{2021.2022}=\frac{1}{2021}\)với \(k\)tự nhiên, \(k< 2021\))
Suy ra \(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(>\frac{1}{2021}+\frac{1}{2021}+...+\frac{1}{2021}=\frac{2021}{2021}=1\)
Suy ra \(1< A\le\frac{2022}{2021}\)do đó \(A\)không phải là số tự nhiên.
DD
Đoàn Đức Hà
Giáo viên
2 tháng 3 2021
a) \(M=2020+2020^2+...+2020^{10}\)
\(M=\left(2020+2020^2\right)+\left(2020^3+2020^4\right)+...+\left(2020^9+2020^{10}\right)\)
\(M=2020\left(1+2020\right)+2020^3\left(1+2020\right)+...+2020^9\left(1+2020\right)\)
\(M=2021\left(2020+2020^3+...+2020^9\right)⋮2021\).
b) Bạn làm tương tự câu a).
2 tháng 3 2021
b, \(A=2021+2021^2+...+2021^{2020}\)
\(=2021\left(1+2021\right)+...+2021^{2019}\left(1+2021\right)\)
\(=2022\left(2021+...+2021^{2019}\right)⋮2022\)
Vậy ta có đpcm
15 tháng 6 2023
B/A
\(=\dfrac{1+\dfrac{2020}{2}+1+\dfrac{2019}{3}+...+1+\dfrac{1}{2021}+1}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}\)
\(=\dfrac{2022\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}=2022\)
LP
2
24 tháng 2 2022
\(2A=\dfrac{2^{2021}-1-1}{2^{2021}-1}=1-\dfrac{1}{2^{2021}-1}\)
\(2B=\dfrac{2^{2022}-1-1}{2^{2022}-1}=1-\dfrac{1}{2^{2022}-1}\)
mà \(2^{2021}-1< 2^{2022}-1\)
nên A<B
27 tháng 2 2022
A=22020−122021−1A=22020-122021-1
⇒2A=2.(22020−1)22021−1⇒2A=2.(22020-1)22021-1
⇒2A=22021−222021−1⇒2A=22021-222021-1
⇒2A=22021−1−122021−1⇒2A=22021-1-122021-1
⇒2A=1−122021−1⇒2A=1-122021-1
B=22021−122022−1B=22021-122022-1
⇒2B=2.(22021−1)22022−1⇒2B=2.(22021-1)22022-1
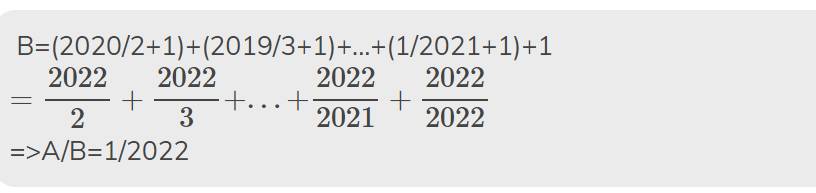
a) Ta có A = 1 + 21 + 22 + ... + 22021
2A = 21 + 22 + 23 + ... + 22022
Vậy 2A = 21 + 22 + 23 + ... + 22022
b) 2A - A = ( 21 + 22 + 23 + ... + 22022 ) - ( 1 + 21 + 22 + ... + 22021 )
A = 22022 - 1
Vậy A = 22022 - 1
a)
\(A=1+2^1+2^2+2^3+...+2^{2020}+2^{2021}\)
\(2A=2^1+2^2+2^3+2^4+...+2^{2021}+2^{2022}\)
b)
\(2A=2^1+2^2+2^3+...+2^{2022}\)
\(2A-A=\left(2^1+2^2+2^3+...+2^{2022}\right)-\left(1+2^1+2^2+....+2^{2021}\right)\)
\(A=2^{2022}-1\)
=> đpcm