K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 3 2017
Gọi \(\dfrac{12}{23}+\dfrac{12}{2323}-\dfrac{121212}{232323}\) là A
Ta sẽ tính biểu thức A.\(\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{7}{12}\right)\)=A.\(\left(\dfrac{7}{12}-\dfrac{7}{12}\right)=0\)
Vậy \(\left(\dfrac{12}{23}+\dfrac{12}{2323}-\dfrac{121212}{232323}\right).\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{7}{12}\right)\)=0
21 tháng 7 2017
+) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\)
\(\Rightarrow2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\right)\)
\(\Rightarrow A=1-\dfrac{1}{2^{10}}=\dfrac{2^{10}-1}{2^{10}}\)
Vậy \(A=\dfrac{2^{10}-1}{2^{10}}\)
+) \(F=\dfrac{1}{15}+\dfrac{1}{21}+\dfrac{1}{28}+...+\dfrac{1}{190}\)
\(\Rightarrow\dfrac{1}{2}F=\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+...+\dfrac{1}{380}\)
\(=\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{19.20}=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{20}\)
\(=\dfrac{1}{5}-\dfrac{1}{20}=\dfrac{3}{20}\Rightarrow F=\dfrac{3}{20}:\dfrac{1}{2}=\dfrac{3}{10}\)
Vậy \(F=\dfrac{3}{10}\)
+) \(G=\dfrac{12}{84}+\dfrac{12}{210}+\dfrac{12}{390}+...+\dfrac{12}{2100}\)
\(=\dfrac{4}{28}+\dfrac{4}{70}+\dfrac{4}{130}+...+\dfrac{4}{700}=\dfrac{4}{4.7}+\dfrac{4}{7.10}+...+\dfrac{4}{25.28}\)
\(=\dfrac{4}{3}.\left(\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{25.28}\right)\)
\(=\dfrac{4}{3}.\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{25}-\dfrac{1}{28}\right)\)
\(=\dfrac{4}{3}.\left(\dfrac{1}{4}-\dfrac{1}{28}\right)=\dfrac{4}{3}.\dfrac{3}{14}=\dfrac{2}{7}\)
Vậy \(G=\dfrac{2}{7}\)
21 tháng 7 2017
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\)
\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\)
\(2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\right)\)
\(A=1-\dfrac{1}{2^{10}}=\dfrac{1024-1}{1024}=\dfrac{1023}{1024}\)
\(F=\dfrac{1}{15}+\dfrac{1}{21}+\dfrac{1}{28}+...+\dfrac{1}{190}\)
\(=\dfrac{2}{30}+\dfrac{2}{42}+\dfrac{2}{56}+...+\dfrac{2}{380}\)
\(=\dfrac{2}{5.6}+\dfrac{2}{6.7}+\dfrac{2}{7.8}+...+\dfrac{2}{19.20}\)
\(=2\left(\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{19.20}\right)\)
\(=2\left(\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)\)
\(=2\left(\dfrac{1}{5}-\dfrac{1}{20}\right)=2.\dfrac{3}{20}=\dfrac{3}{10}\)
\(G=\dfrac{12}{84}+\dfrac{12}{210}+\dfrac{12}{390}+...+\dfrac{12}{2100}\)
\(=\dfrac{4}{28}+\dfrac{4}{70}+\dfrac{4}{130}+...+\dfrac{4}{700}\)
\(=\dfrac{4}{4.7}+\dfrac{4}{7.10}+\dfrac{4}{10.13}+...+\dfrac{4}{25.28}\)
\(=\dfrac{4}{3}\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+...+\dfrac{1}{25}-\dfrac{1}{28}\right)\)
\(=\dfrac{4}{3}\left(\dfrac{1}{4}-\dfrac{1}{28}\right)\)
\(=\dfrac{4}{3}.\dfrac{3}{14}=\dfrac{2}{7}\)
14 tháng 4 2017
\(-1\dfrac{1}{5}.\dfrac{12+\dfrac{4}{3}-\dfrac{12}{37}-\dfrac{12}{35}}{3+\dfrac{1}{3}-\dfrac{3}{37}-\dfrac{3}{35}}:\dfrac{4+\dfrac{4}{17}+\dfrac{4}{19}+\dfrac{4}{2003}}{5+\dfrac{5}{17}+\dfrac{5}{19}+\dfrac{5}{2003}}\)
\(=\dfrac{-6}{5}.\dfrac{4\left(3+\dfrac{1}{3}-\dfrac{3}{37}-\dfrac{3}{35}\right)}{3+\dfrac{1}{3}-\dfrac{3}{37}-\dfrac{3}{35}}:\dfrac{4\left(1+\dfrac{1}{17}+\dfrac{1}{19}+\dfrac{1}{2003}\right)}{5\left(1+\dfrac{1}{17}+\dfrac{1}{19}+\dfrac{1}{2003}\right)}\)
\(=\dfrac{-6}{5}.4:\dfrac{4}{5}\)
\(=\dfrac{-6.4.5}{5.4}=-6\)
Q
17 tháng 4 2017
a) \(\dfrac{1}{3}+\dfrac{3}{8}-\dfrac{7}{12}\)
\(=\dfrac{17}{24}-\dfrac{7}{12}\)
\(=\dfrac{1}{8}\)
b) \(\dfrac{-3}{14}+\dfrac{5}{8}-\dfrac{1}{2}\)
\(=\dfrac{23}{56}-\dfrac{1}{2}\)
\(=\dfrac{-5}{56}\)
c) \(\dfrac{1}{4}-\dfrac{2}{3}-\dfrac{11}{18}\)
\(=\dfrac{-5}{12}-\dfrac{11}{18}\)
\(=\dfrac{-37}{36}\)
d) \(\dfrac{1}{4}+\dfrac{5}{12}-\dfrac{1}{13}-\dfrac{7}{8}\)
\(=\dfrac{2}{3}-\dfrac{1}{13}-\dfrac{7}{8}\)
\(=\dfrac{23}{39}-\dfrac{7}{8}\)
\(=\dfrac{-89}{312}\)
23 tháng 7 2017
Các bạn không cần trả lời câu hỏi trên của mik vì mik đã hiểu rồi nha . Cho nên đừng trả lời ! OK
KL
26 tháng 7 2017
a, \(4\times\left(-\dfrac{1}{2}\right)^3-2\times\left(-\dfrac{1}{2}\right)^2+3\times\left(-\dfrac{1}{2}\right)+1\)
\(=\left(-\dfrac{1}{2}\right)\left[\left(4\times-\dfrac{1}{2}\right)-\left(2\times-\dfrac{1}{2}\right)+3\right]+1\)
\(=\left(-\dfrac{1}{2}\right)\left(-2+1+3\right)+1\)
\(=\left(-\dfrac{1}{2}\right)2+1\)
\(=-1+1\)
\(=0\)
@Trịnh Thị Thảo Nhi
29 tháng 4 2018
a, 4×(−12)3−2×(−12)2+3×(−12)+14×(−12)3−2×(−12)2+3×(−12)+1
=(−12)[(4×−12)−(2×−12)+3]+1=(−12)[(4×−12)−(2×−12)+3]+1
=(−12)(−2+1+3)+1=(−12)(−2+1+3)+1
=(−12)2+1=(−12)2+1
=−1+1=−1+1
=0=0
15 tháng 6 2018
a, \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{9900}\)
\(\Rightarrow\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)
\(\Rightarrow\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{100}\)
\(\Rightarrow\dfrac{1}{1}-\dfrac{1}{100}\)
\(\Rightarrow\dfrac{99}{100}\)
21 tháng 6 2017
Đây này má Ran mori
a) \(\left(5\dfrac{1}{7}-3\dfrac{3}{11}\right)-2\dfrac{1}{7}-1\dfrac{8}{11}\)
\(=5+\dfrac{1}{7}-3-\dfrac{3}{11}-2-\dfrac{1}{7}-1-\dfrac{8}{11}\)
\(=\left(5-3-2-1\right)+\left(\dfrac{1}{7}-\dfrac{3}{11}-\dfrac{1}{7}-\dfrac{8}{11}\right)\)
\(=-1+\left(\dfrac{1}{7}-\dfrac{1}{7}\right)-\left(\dfrac{3}{11}+\dfrac{8}{11}\right)\)
\(=-1+0-1=-2\)
RM
21 tháng 6 2017
a)\(\left(5\dfrac{1}{7}-3\dfrac{3}{11}\right)-2\dfrac{1}{7}-1\dfrac{8}{11}\)
= \(\left(5+\dfrac{1}{7}-3+\dfrac{3}{11}\right)-2+\dfrac{1}{7}-1+\dfrac{8}{11}\)
= \(5-\dfrac{1}{7}+3-\dfrac{3}{11}-2+\dfrac{1}{7}-1+\dfrac{8}{11}\)
= \(\left(5-3-2-1\right)+\dfrac{1}{7}+\dfrac{1}{7}+\dfrac{8}{11}-\dfrac{3}{11}\)
= \(-1+2+\dfrac{5}{11}\)
= \(1+\dfrac{5}{11}=\dfrac{1}{1}+\dfrac{5}{11}=\dfrac{11}{11}+\dfrac{5}{11}=\dfrac{16}{11}\)
Vậy :câu a) = \(\dfrac{16}{11}\)
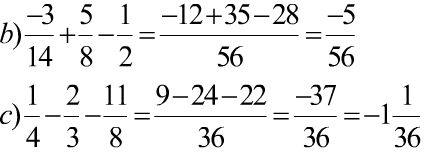
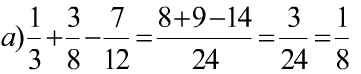
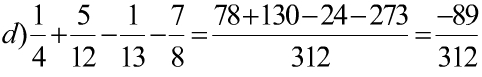
\(12-12\dfrac{1}{3}=12-\dfrac{12\times3+1}{3}=12-\dfrac{37}{3}=\dfrac{12\times3-37}{3}=\dfrac{36-37}{3}=\dfrac{-1}{3}\)
= 12 và 2/3\(\dfrac{ }{ }\)