
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có hằng đẳng thức:
\(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
Ta thấy \(\left(x-1\right)+\left(x-2\right)+\left(3-2x\right)=0\)
do đó \(\left(x-1\right)^3+\left(x-2\right)^3+\left(3-2x\right)^3=3\left(x-1\right)\left(x-2\right)\left(3-2x\right)\)
suy ra \(\left(x-1\right)\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x_1=1\\x_2=2\\x_3=\frac{3}{2}\end{cases}}\)
\(S=\frac{29}{4}\).

Nghiệm chung của hai bất phương trình là 3 ≤ x ≤ 6.
Vì x ∈ Z nên n ∈ {3; 4; 5}.

Vì phương trình nghiệm đúng với mọi x nên tập nghiệm của nó là S = R.

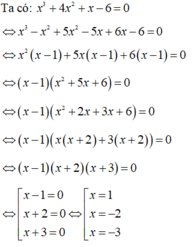
Tích các nghiệm của phương trình đã cho là: 1 . (-2) . (-3) = 6
Đáp án cần chọn là D

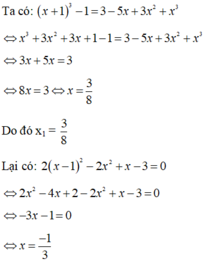
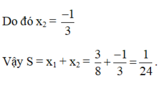


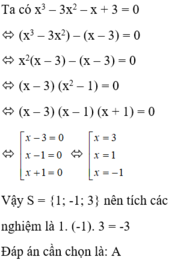
\(x^3+1=x\left(x+1\right)\Rightarrow x^3-x^2-x+1=0\)
Dễ thấy x= 1 là nghiệm
suy ra nghiệm còn lại là -1
có thể tham khảo thêm tại https://vn.answers.yahoo.com/question/index?qid=20110613202327AAXGfpF
chuyển vế và xếp lại có:
x3 - x2 -x +1 = x2(x-1) - (x-1) =(x2-1)(x-1) =0
vậy pt có 2 nghiệm là: x = -1 và x =1