


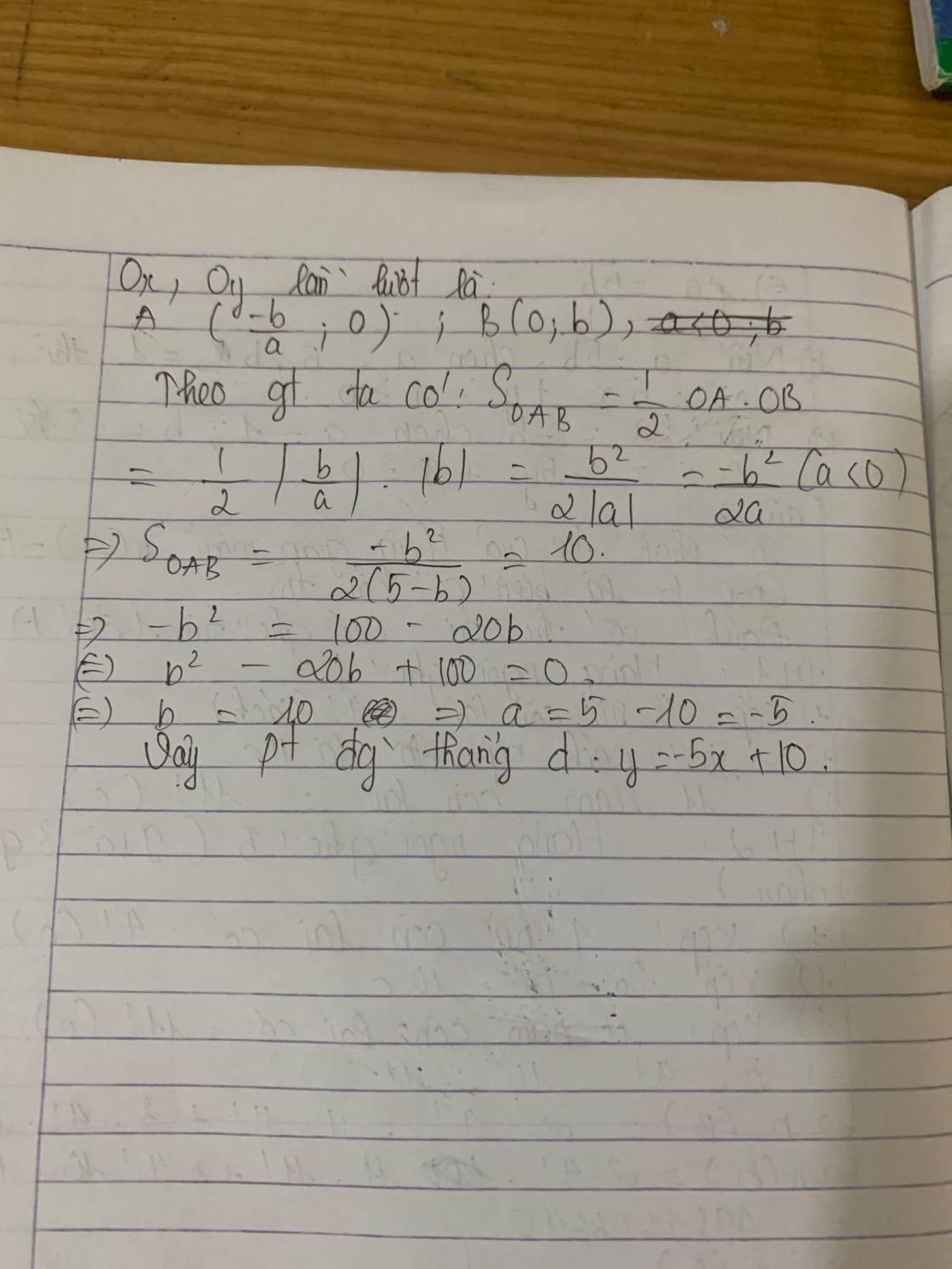
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



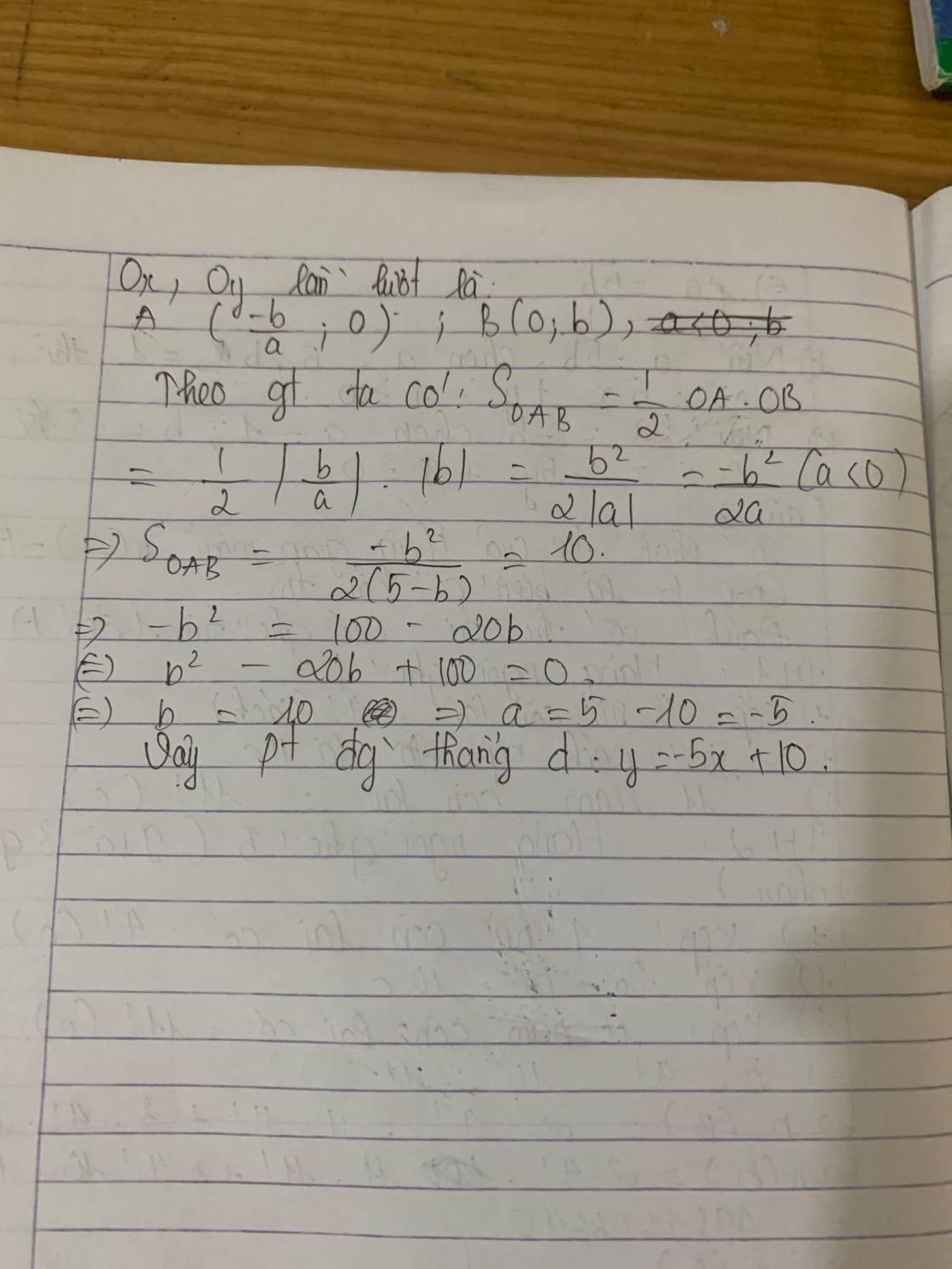

Do d qua K nên pt d có dạng: \(y=kx-k+3\) (với \(k\ne0;3\))
Gọi A và B lần lượt là giao điểm của d với Ox; Oy
\(\Rightarrow\left\{{}\begin{matrix}A\left(\dfrac{k-3}{k};0\right)\\B\left(0;-k+3\right)\end{matrix}\right.\)
Để A; B có hoành độ dương (do nằm trên các tia Ox; Oy) \(\Rightarrow k< 0\)
Khi đó: \(OA=\dfrac{k-3}{k}\) ; \(OB=-k+3\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=6\Leftrightarrow\dfrac{\left(k-3\right)\left(-k+3\right)}{k}=12\)
\(\Leftrightarrow k^2+6k+9=0\Leftrightarrow k=-3\)
Phương trình d: \(y=-3x+6\)

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

Gọi pt đường thẳng có dạng: \(y=ax+b\)
Đường thẳng qua M nên: \(6=-a+b\Rightarrow b=a+6\)
\(\Rightarrow y=ax+a+6\)
Đường thẳng cắt 2 tia Ox, Oy khi \(a\ne\left\{-6;0\right\}\)
Gọi A là giao điểm với Ox \(\Rightarrow A\left(-\dfrac{a+6}{a};0\right)\) \(\Rightarrow OA=\left|x_A\right|=\left|\dfrac{a+6}{a}\right|\)
Gọi B là giao điểm với Oy \(\Rightarrow B\left(0;a+6\right)\Rightarrow OB=\left|y_B\right|=\left|a+6\right|\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}\left|\dfrac{a+6}{a}\right|.\left|a+6\right|=4\)
\(\Leftrightarrow\left|\dfrac{a^2+12a+36}{a}\right|=8\Rightarrow a^2+20a+36=0\)
\(\Rightarrow\left[{}\begin{matrix}a=-2\\a=-18\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=-2x+4\\y=-18x-12\end{matrix}\right.\)