Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta AHB\) vuông tại H và \(\Delta AHC\) vuông tại H:
AB = AC (\(\Delta ABC\) cân tại A).
\(\widehat{B}=\widehat{C}\) (\(\Delta ABC\) cân tại A).
\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - góc nhọn).
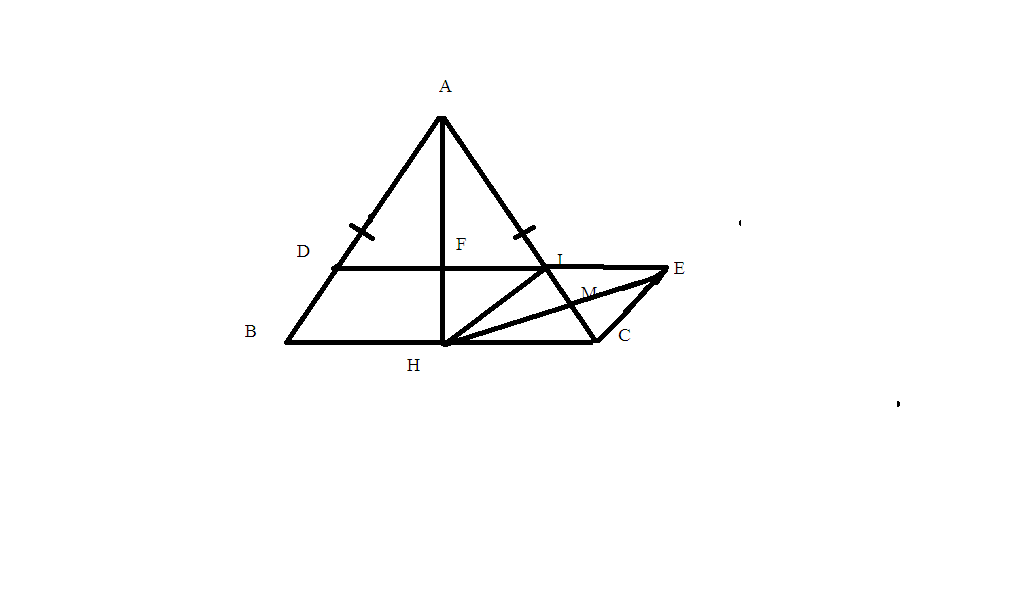
b) Xét \(\Delta DHC:\)
DI là trung tuyến (I là trung điểm của HC).
DI là đường cao \(\left(DI\perp HC\right).\)
\(\Rightarrow\Delta DHC\) cân tại D.

Lần sau chép đề cẩn thận nhé. Sai tùm lum.
a, ΔAHB = ΔAHC.
Xét hai tam giác vuông AHB và AHC có:
AB = AC (hai cạnh bên)
^B = ^C (hai góc ở đáy)
Do đó: ΔAHB = ΔAHC (cạnh huyền - góc nhọn)
b, ΔDHC cân. DM//AH. (sửa M là trung điểm HC nhé ! )
Vì HD//BA (gt) => ^B = ^H1 (đồng vị)
Mà ^B = ^C => ^H1 = ^C => ΔDHC cân tại D (hai góc ở đáy)
Xét ΔDHM và ΔDCM có:
DH = DC (hai cạnh bên)
HM = MC (M là trung điểm của HC)
DM : chung
Do đó: ΔDHM = ΔDCM (c.c.c)
=> ^M1 = ^M2 (hai góc tương ứng)
Mà ^M1 + ^M2 = 180o (kề bù)
=> ^M1 = ^M2 = 180o : 2 = 90o hay DM ⊥ BC.
Vậy DM // AH (cùng vuông góc với BC).
c, G là trọng tâm ΔABC. AH + BD > 3HD.
Ta có: ^H2 = ^A1 (so le trong)
Mà ^A1 = ^A2 (hai góc tương ứng)
=> ^H2 = ^A2 => ΔHDA cân tại D (hai góc ở đáy)
=> DA = DH (hai cạnh bên)
Vì DH = DC (hai cạnh bên)
DA = DH (hai cạnh bên)
=> DA = DC
=> BD là trung tuyến ứng với cạnh bên AC.
Vì BH = HC (hai cạnh tương ứng) => AH là trung tuyến ứng với cạnh đáy BC.
Mà AC cắt BC tại G => CG là trung tuyến ứng với cạnh bên AB
=> G là trọng tâm của ΔABC.

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét ΔABC có
H là trung điểm của CB
HD//AB
=>D là trung điểm của AC
ΔAHC vuông tại H có HD là trung tuyến
nên DH=DC
=>ΔDHC cân tại D
=>DM vuông góc HC
=>DM//AH

a) Xét ΔABH và ΔACH có:
AB=AC (ΔABC cân tại A)
AH là cạnh chung
HB=HC(H là trung điểm của BC)
Nên ΔABH =ΔACH (c.c.c)
=>\(\widehat{AHB}=\widehat{AHC}\)( 2 GÓC TƯƠNG ỨNG)
Ta có: \(\widehat{AHB}+\widehat{AHC}=180^O\)( 2 góc kề bù)
=>\(\widehat{AHB}.2=180^O\Rightarrow\widehat{AHB}=90^O\)
=>AH ⊥ BC
b) Vì ΔABH =ΔACH => \(\widehat{BAH}=\widehat{CAH}\)
Ta có: AD+BD=AB ( D nằm giữa A và B)
AI+IC=AC( I nằm giữa A và C)
Mà AB=AC, BD=IC =>AD=AI
Cho AH và DI cắt nhau tại F
Xét ΔDFA và ΔIFA có:
FA là cạnh chung
\(\widehat{BAH}=\widehat{CAH}\)
AD=AI
Nên ΔDFA=ΔIFA (c.g.c)
=>\(\widehat{DAF}=\widehat{IAF}\)
=>A là tia phân giác của góc DHI

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét ΔMAD và ΔMBH có
góc MAD=góc MBH
MA=MB
góc AMD=góc BMH
=>ΔMAD=ΔMBH
=>AD=BH
mà AD//BH
nên ADBH là hình bình hành
=>BD=AH
O x và y khác nhau ở điểm truc nên ta có phuong trình x +y bằng 65% tỉ lệ hành hóa