TD
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
0
11 tháng 2 2020
a) Vẽ OK là tia phân giác của góc BOC
Ta có : ∠ BOC = 180o - ( ∠ OBC + ∠OCB )
Mà ∠OBC = 1212. ∠ABC
∠OCB = 1212.∠ACB
=> ∠BOC = 180o-1/2x(∠ABC + ∠ ACB )
Mặt khác , ∠ABC + ∠ACB = 180o - ∠A = 180 o - 60o = 120o
=> ∠BOC = 180o- 1212. 120o = 120o
Ta có : ∠EOB + ∠BOC = 180o ( 2 góc kề bù )
=>∠EOB = 180o - 120o = 60o (1)
∠DOC + ∠BOC = 180o (2 góc kề bù )
=> ∠DOC = 180o - 120o = 60o (2)
Từ (1) và (2) => ∠EOB = ∠DOC (= 60o) ( 3)
Vì OK là tia phân giác của góc BOC nên ∠BOK = ∠COK = 1/2x 120o = 60o (4)
Từ (3) và (4) => ∠BOK = ∠ COK = ∠EOB =∠DOC
Xét ΔEOB và Δ KOB có :
OB : cạnh chung
∠EBO = ∠OBK ( gt)
∠EOB = ∠BOK (cmt)
=> ΔEOB = Δ KOB(g - c - g)
=> OE = OK ( 2 cạnh tương ứng) (5)
Xét ΔDOC và ΔKOC có :
OC : cạnh chung
∠KCO = ∠OCD ( gt)
∠KOC = ∠COD ( cmt)
=> ΔDOC = ΔKOC ( g - c - g)
=> OK = OD( 2 cạnh t/ứng) (6)
Từ (5) và (6) => OD = OE ( = OK)
Xét ΔDOE có OD = OE nên ΔDOE cân tại O
b)Vì ΔEOB = Δ KOB (cm câu a)
=> BE = BK ( 2 cạnh t/ứng)
Vì ΔDOC = ΔKOC ( cm câu a)
=> CD = CK ( 2 cạnh t/ứng )
Ta có : BE = BK (cmt)
CD = CK (cmt)
=> BE + CD = BK + CK = BC ( đpcm)
11 tháng 2 2020
cai so 1212 do bi loi nen ban phai doi thanh \(\frac{1}{2}\)cho mk nha
dau cham la dau nhan
13 tháng 4 2016
B1: Vì M là đường phân giác => A1 = A2 ( bạn đánh số 1,2 ở 2 phần góc chỗ góc A nhé)
Mà AB = AC ; góc B = góc C ( gt ) => Tam giác ABM = tam giác AMC mà 2 tam giác này có AM chung => AM là đg trung tuyến
13 tháng 4 2016
b1: tự làm dc
b2:goi gd bd la x
:theo dinh li pi-ta-go:
ba+ad=bd
hay ba + 1/2x=x
ba=x-1/2x
ba=x*1/2
3=x*1/2
x=3:1/2=1.5
13 tháng 4 2016
B2 khó v~ bạn ơi lm mãi 0 ra cái hình mik vẽ hoặc là sai hoặc là mik chưa lm đúng xin lỗi bạn nhưng theo mik thì mấy dạng bài như vầy th`g thì sẽ = 3 cũng chính là dữ kiện số do duy nhất trong bài
15 tháng 6 2018
a, Xét ∆ ABC vuông tại A
➡️AB2 + AC2 = BC2 (Pitago)
➡️BC2 = 32 + 42
➡️BC2 = 25
➡️BC = 5 (cm)
b, Xét ∆ ABD và ∆ EBD có:
Góc A = góc E = 90°
BD chung
Góc ABD = góc EBD (gt)
➡️∆ ABD = ∆ EBD (ch - gn)
➡️AB = EB (2 cạnh t/ư)
c, Ta có:
BA + AK = BK
BE + EC = BC
mà AB = EB (cmt)
AK = EC (gt)
➡️BK = BC
Xét ∆ BKI và ∆ BCI có:
BK = BC (cmt)
Góc ABD = góc EBD (gt)
BI chung
➡️∆ BKI = ∆ BCI (c.g.c)
➡️Góc BKI = góc BCI (2 góc t/ư)
d, Xét ∆ ABI và ∆ EBI có:
AB = EB (cmt)
Góc ABD = góc EBD (gt)
BI chung
➡️∆ ABI = ∆ EBI (c.g.c)
➡️IA = IE (2 cạnh t/ư)
Hok tốt~
PL
13 tháng 8 2017
bạn tự vẽ hình nha
a) Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại A
=> \(AB^2+AC^2=BC^2\)
\(3^2+4^2=BC^2\)
\(9+16=BC^2\)
=> \(BC^2=25\)
=>\(BC=5\)
b) Xét tam giác ABD và tam giác EBD có:
\(\widehat{BAD}=\widehat{BED}\left(=90độ\right)\)
BD chung
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
=> tam giác ABD = tam giác EBD (ch-gn)
c)Vì tam giác ABD = tam giác EBD
=>\(BA=BE\left(1\right)\)
Theo đề bài ta có:
\(AK=EC\left(2\right)\)
Cộng 2 vế của (1),(2)
=>\(BA+AK=BE+EC\)
\(BK=BE\)
=> tam giác BKC cân
=>\(\widehat{BKC}=\widehat{BCK}\)
d)Xét tam giác BAI và tam giác BEI có:
IB chung
\(\widehat{ABI}=\widehat{EBI}\left(gt\right)\)
\(AB=BE\)
=> tam giác BAI = tam giác BEI (c-g-c)
=>AI = EI
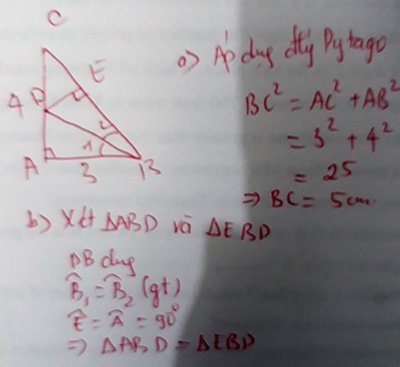
Ghi rõ đề bài nha bạn !
Vì BD là phân giác góc B => góc ABD=1/2 góc B = 30 độ
góc A=90 độ
=> Tam giác ABD là nửa tam giác đều cạnh BD
=> AB=\(\dfrac{BD\sqrt{3}}{2}\)
=> \(BD=\dfrac{2AB}{\sqrt{3}}=2\sqrt{3}\)