K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LD
27 tháng 4 2022
Đáp án:
Giải thích các bước giải:
a) F(x) = 3x – 6
F(x) = 0 ⇔ 3x – 6 = 0
⇔ 3x = 6
⇔ x = 2
b) U(y) = -5y + 30
U(y) = 0 ⇔ -5y + 30 = 0
⇔ -5y = -30
⇔ y = 6
c) G(z) = (z – 3) (16 – 4z)
G(z) = 0 ⇔
)
⇔
YN
27 tháng 4 2022
a) Để cho đa thức F(x) có nghiệm thì \(3x-6=0\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=6:3\)
\(\Rightarrow x=2\)
b) Để cho đa thức U(y) có nghiệm thì \(-5y+30=0\)
\(\Rightarrow-5y=30\)
\(\Rightarrow y=30:-5\)
\(\Rightarrow y=6\)
c) Để cho đa thức G(z) có nghiệm thì \(\left(z-3\right)\left(16-4z\right)=4\left(z-3\right)\left(4-z\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}z-3=0\\4-z=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}z=3\\z=4\end{matrix}\right.\)
LT
1
TH
8 tháng 1 2018
a)
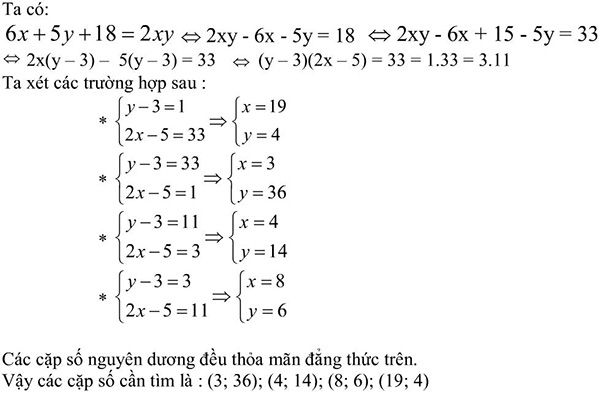
b)
Nhận thấy: x phải là số lẻ. Vì nếu x là số chẵn thì 3x^2 sẽ là số chẵn => 3x^2-4y^2 là số chẵn trong khi 13 là số lẻ
x là số lẻ => x có dạng x= 2k+1 với k thuộc Z
thay x=2k+1 vào phương trình ta có:
3(4k^2+4k+1) - 4y^2 = 13
<=> 6k^2+6k-2y^2=5
<=> 6k(k+1) = 5+2y^2
Dễ thấy vế trái là số chẵn trong khi vế phải là số lẻ => phương trình không có nghiệm nguyên => dpcm
HT
1
HN
11 tháng 3 2019
\(-x^5y^3-3x^4y^3+x^4y^3-4x^5y^3-6xy^2+5x^5y^3\)
Bậc của đa thức là: 8
Vì ở đây có 2 số mũ có tổng lớn nhất là 5 và 3
Mà 5 + 3 = 8
\(\Rightarrow\)Bậc của đa thức là: 8
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) Thay \(x = 2\) vào đa thức \(P(x) = 3x - 4\) ta được: \(P(2) = 3.2 - 4 = 6 - 4 = 2\).
Thay \(x = \dfrac{4}{3}\) vào đa thức \(P(x) = 3x - 4\) ta được: \(P(\dfrac{4}{3}) = 3.\dfrac{4}{3} - 4 = 4 - 4 = 0\).
Vậy x = 2 không là nghiệm của đa thức \(P(x) = 3x - 4\); \(x = \dfrac{4}{3}\)là nghiệm của đa thức \(P(x) = 3x - 4\).
b)Thay \(y = 1\) vào đa thức \(Q(y) = {y^2} - 5y + 4\) ta được: \(Q(1) = {1^2} - 5.1 + 4 = 1 - 5 + 4 = 0\).
Thay \(y = 4\) vào đa thức \(Q(y) = {y^2} - 5y + 4\) ta được: \(Q(4) = {4^2} - 5.4 + 4 = 16 - 20 + 4 = 0\).
Vậy \(y = 1,y = 4\)là nghiệm của đa thức \(Q(y) = {y^2} - 5y + 4\).
NT
3
16 tháng 8 2016
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{3x-1}{5}=\frac{5y-2}{7}=\frac{3x+5y-3}{4x}=\frac{\left(3x-1\right)+\left(5y-2\right)}{5+7}=\frac{3x+5y-3}{12}.\)
\(\frac{3x+5y-3}{4x}=\frac{3x+5y-3}{12}\Rightarrow4x=12\Rightarrow x=3\)