D
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 10 2021
1, Vì \(a\perp BC;b\perp BC\) nên a//b
2, Ta có \(\widehat{A_1}=\widehat{A_2}=60^0\left(đối.đỉnh\right)\)
Vì a//b nên \(\widehat{A_2}=\widehat{D_1}=60^0\left(đồng.vị\right)\)
Ta có \(\widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_2}=180^0-60^0=120^0\)
CM
19 tháng 7 2019
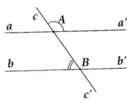
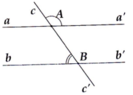
Ta có: c A a ' ^ + a ' A B ^ = 180° (hai góc kề bù)
=> a ' A B ^ = 180 ° − c A a ' ^ = 180 ° − 120 ° = 60 °
=> a ' A B ^ = A B b ^ = 60 ° (hai góc so le trong bằng nhau)
=> aa' // bb'
HL
1
CM
5 tháng 5 2018
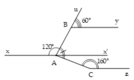
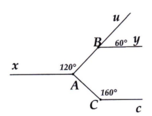
Kẻ tia Ax' là tia đối của tia Ax
Khi đó:
x ' A B ^ = u B y ^ = 60 °
⇒ A x ' // B y
Cũng có:
x ' A C ^ = 80 ° − 60 ° = 20 ° .
⇒ x ' A C ^ + A C z ^ = 180 °
⇒ A x ' // C z .
Do đó các tia A x , B y , C z nằm trên ba đường thẳng song song với nhau
BH
1
6 tháng 8 2021
a'a không song song với b'b
Vì ở vị trí đồng vị cMa ko bằng MNb
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
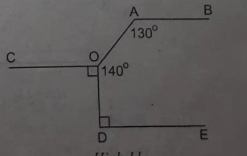
a) Vì a,b cùng vuông góc với đường thẳng AB nên a // b
b) Vì \(\widehat {{B_1}} = \widehat {{C_2}}( = 40^\circ )\). Mà 2 góc này ở vị trí so le trong nên b // c ( Dấu hiệu nhận biết 2 đường thẳng song song)
c) Vì a // b, b //c nên a // c
15 tháng 10 2021
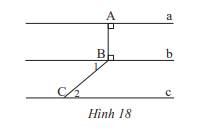
Ta có \(\widehat{B_1}=\widehat{B_3}=47^0\left(đối.đỉnh\right)\)
\(\Rightarrow\widehat{B_3}+\widehat{A_1}=47^0+133^0=180^0\)
Mà 2 góc này ở vị trí trong cùng phía nên a//b
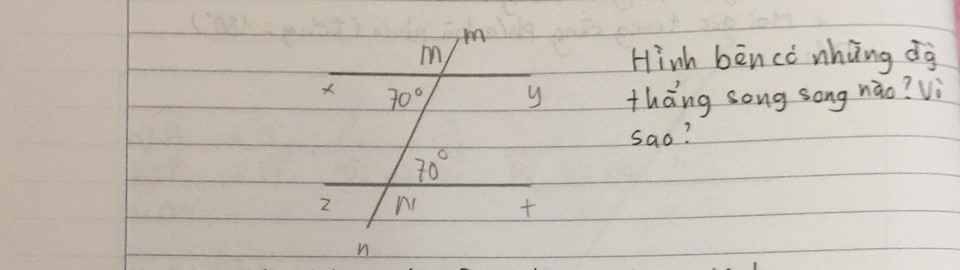
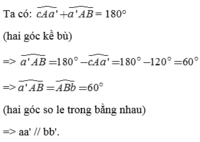
Vì góc xmn và góc mnt là 2 góc so le trong và đều bằng 70o
=> 2 đt xy // zt