Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M=\dfrac{8}{3}\cdot\dfrac{2}{5}\cdot\dfrac{3}{8}\cdot10\cdot\dfrac{19}{92}\\ =\dfrac{8\cdot2\cdot3\cdot10\cdot19}{3\cdot5\cdot8\cdot92}\\ =\dfrac{8\cdot2\cdot3\cdot2\cdot5\cdot19}{3\cdot5\cdot8\cdot2\cdot2\cdot23}\\ =\dfrac{19}{23}\)
\(N=\dfrac{5}{7}\cdot\dfrac{5}{11}+\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{14}{11}\\ =\dfrac{5}{7}\cdot\left(\dfrac{5}{11}+\dfrac{2}{11}-\dfrac{14}{11}\right)\\ =\dfrac{5}{7}\cdot\left(-\dfrac{7}{11}\right)\\ =-\dfrac{5}{11}\)
\(Q=\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot\left(\dfrac{1}{6}-\dfrac{1}{6}\right)\\ =\left(\dfrac{1}{99}+\dfrac{12}{999}-\dfrac{123}{9999}\right)\cdot0\\ =0\)

A=2.(1/1.3 + 1/3.5 + 1/5.7 +.......+1/99.101)
=2.(1/1 + 1/3 + 1/5 + 1/5 + 1/7 +...+1/99 + 1/101)
=2.(1-1/101)
=2.(101/101-1/101)
=2.100/101
200/101
B=2.(1/1.3+1/3.5+1/3.1+....+1/99.101)
=2.(1/1+1/3+1/3+1/5+1/3+1/7+....+1/99+1/101)
=2.(1/1+1/101)
=2.(101/101+1/101)
=2.102/101
=204/101

a) \(1-\dfrac{1}{2}=\dfrac{1}{2}\)
\(\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{3-2}{6}=\dfrac{1}{6}\)
\(\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{4-3}{12}=\dfrac{1}{12}\)
\(\dfrac{1}{4}-\dfrac{1}{5}=\dfrac{5-4}{20}=\dfrac{1}{20}\)
\(\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{6-5}{30}=\dfrac{1}{30}\)
b) \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}\)
\(=\left(1-\dfrac{1}{2}\right)+\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\left(\dfrac{1}{3}-\dfrac{1}{4}\right)+\left(\dfrac{1}{4}-\dfrac{1}{5}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}\right)\)
\(=1+\left(-\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(-\dfrac{1}{4}+\dfrac{1}{4}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+-\dfrac{1}{6}\)\(=1+-\dfrac{1}{6}\)
\(=\dfrac{5}{6}\)

Các câu dễ tự làm nha:
\(D=\dfrac{1}{100.99}-\dfrac{1}{99.98}-\dfrac{1}{98.97}-...-\dfrac{1}{3.2}-\dfrac{1}{2.1}\)
\(D=\dfrac{1}{99}-\dfrac{1}{100}-\dfrac{1}{99}+\dfrac{1}{98}-\dfrac{1}{98}+\dfrac{1}{97}-...-\dfrac{1}{2}+\dfrac{1}{3}-1+\dfrac{1}{2}\)\(D=-\dfrac{1}{100}-1\)

a: \(=\left(\dfrac{19}{6}-\dfrac{2}{5}\right):\left(\dfrac{29}{6}+\dfrac{7}{10}\right)\)
\(=\dfrac{19\cdot5-2\cdot6}{30}:\dfrac{290+42}{30}=\dfrac{83}{332}=\dfrac{1}{4}\)
b: \(=\dfrac{\left(\dfrac{102}{25}-\dfrac{2}{25}\right)\cdot\dfrac{17}{4}}{\left(6+\dfrac{5}{9}-3-\dfrac{1}{4}\right)\cdot\dfrac{16}{7}}\)
\(=\dfrac{4\cdot\dfrac{17}{4}}{\dfrac{16}{7}\cdot\dfrac{119}{36}}=\dfrac{17}{\dfrac{68}{9}}=17\cdot\dfrac{9}{68}=\dfrac{9}{4}\)
c: \(=\left(\dfrac{120}{60}-\dfrac{15}{60}+\dfrac{20}{60}-\dfrac{36}{60}\right):\left(\dfrac{45}{15}-\dfrac{3}{15}-\dfrac{25}{15}\right)\)
\(=\dfrac{89}{60}:\dfrac{17}{15}=\dfrac{89}{60}\cdot\dfrac{15}{17}=\dfrac{89}{68}\)

a) Hình như nhầm đề thì phải :v
\(P=\dfrac{\dfrac{2}{3}-\dfrac{1}{4}+\dfrac{5}{11}}{\dfrac{5}{12}+1-\dfrac{6}{11}}\)
\(=\dfrac{\dfrac{5}{12}+\dfrac{5}{11}}{\dfrac{5}{12}+\dfrac{5}{11}}=1\)
b) \(Q=\dfrac{0,125-\dfrac{1}{5}+\dfrac{1}{7}}{0,375-\dfrac{3}{5}+\dfrac{3}{7}}+\dfrac{\dfrac{1}{2}+\dfrac{1}{3}-0,2}{\dfrac{3}{4}+0,5-\dfrac{3}{10}}\)
\(Q=\dfrac{0,125-\dfrac{1}{5}+\dfrac{1}{7}}{3\left(0,125-\dfrac{1}{5}+\dfrac{1}{7}\right)}+\dfrac{\dfrac{1}{2}+\dfrac{1}{3}-0,2}{\dfrac{3}{4}+0,5-\dfrac{3}{10}}\)
\(Q=\dfrac{1}{3}+\dfrac{\dfrac{1}{2}+\dfrac{1}{3}-0,2}{\dfrac{3}{4}+0,5-\dfrac{3}{10}}\)
\(Q=\dfrac{1}{3}+\dfrac{\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{5}}{\dfrac{3}{2}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{3}\right)}=\dfrac{1}{3}+\dfrac{1}{\dfrac{3}{2}}\)
\(Q=\dfrac{1}{3}+\dfrac{2}{3}=1\)
a,\(P=\dfrac{\dfrac{2}{3}-\dfrac{1}{4}+\dfrac{5}{11}}{\dfrac{5}{12}+1-\dfrac{7}{11}}=\dfrac{\left(\dfrac{2}{3}-\dfrac{1}{4}+\dfrac{5}{11}\right).132}{\left(\dfrac{5}{12}+1-\dfrac{7}{11}\right).132}=\dfrac{88-33+60}{55+132-84}=\dfrac{115}{103}\)
b, Ta có : 0,125 = \(\dfrac{1}{8}\) ; 0,375 = \(\dfrac{3}{8}\) ; 0,2 = \(\dfrac{1}{5}\) ; 0,5 = \(\dfrac{3}{6}\)
\(Q=\dfrac{\dfrac{1}{8}-\dfrac{1}{5}+\dfrac{1}{7}}{\dfrac{3}{8}-\dfrac{3}{5}+\dfrac{3}{7}}+\dfrac{\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{5}}{\dfrac{3}{4}+\dfrac{3}{6}-\dfrac{3}{10}}\)
\(Q=\dfrac{\dfrac{1}{8}-\dfrac{1}{5}+\dfrac{1}{7}}{3\cdot\left(\dfrac{1}{8}-\dfrac{1}{5}+\dfrac{1}{7}\right)}+\dfrac{2\cdot\left(\dfrac{1}{4}+\dfrac{1}{6}-\dfrac{1}{10}\right)}{3\cdot\left(\dfrac{1}{4}+\dfrac{1}{6}-\dfrac{1}{10}\right)}\)
\(Q=\dfrac{1}{3}+\dfrac{2}{3}=1\)

BT1: \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}>\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}>1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{5}{6}\)
Vậy ta suy ra đpcm
1. Ta có :
\(\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{6}>\dfrac{1}{6}+\dfrac{1}{6}+.....+\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{6}< \dfrac{1}{6}.5\)
\(\Leftrightarrow\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{6}< \dfrac{5}{6}\)
\(\rightarrowđpcm\)
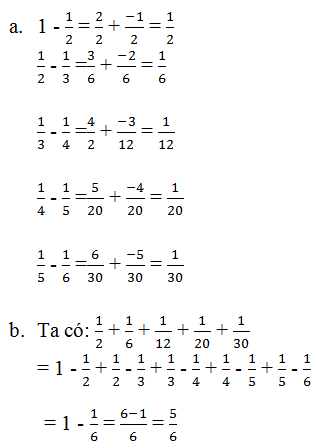
Đặt \(A=\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{10}}\)
\(\Rightarrow5A=1+\dfrac{1}{5}+...+\dfrac{1}{5^9}\)
\(\Rightarrow5A-A=\left(1+\dfrac{1}{5}+...+\dfrac{1}{5^9}\right)-\left(\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{10}}\right)\)
\(\Rightarrow4A=1-\dfrac{1}{5^{10}}\)
\(\Rightarrow A=\dfrac{1-\dfrac{1}{5^{10}}}{4}\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{10}}=\dfrac{1-\dfrac{1}{5^{10}}}{4}\)
\(\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+......+\dfrac{1}{5^{10}}\)
= \(\dfrac{1}{5}\left(1+\dfrac{1}{5}+\dfrac{1}{5^2}+....+\dfrac{1}{5^9}\right)\)
= \(\left[\left(1+\dfrac{1}{5}+\dfrac{1}{5^2}+....+\dfrac{1}{5^9}\right)-\left(\dfrac{1}{5}+\dfrac{1}{5^2}+....+\dfrac{1}{5^{10}}\right)\right]\) : 4
= \(\left(1-\dfrac{1}{10}\right):4\)