Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích các bước giải:
a.Ta có xy//BC,MD//AB��//��,��//��
→AD//BM,AB//DM→ˆBMA=ˆMAD,ˆBAM=ˆAMD→��//��,��//��→���^=���^,���^=���^
Mà ΔABM,ΔMDAΔ���,Δ��� chung cạnh AM��
→ΔABM=ΔMDA(g.c.g)→Δ���=Δ���(�.�.�)
→AD=BM,MD=AB→��=��,��=��
Tương tự chứng minh được AE=MC,ME=AC��=��,��=��
→DE=DA+AE=BM+MC=BC→��=��+��=��+��=��
→ΔABC=ΔMDE(c.c.c)→Δ���=Δ���(�.�.�)
b.Gọi AM∩BD=I��∩��=�
→ˆIAD=ˆIMB,ˆIDA=ˆIBM(AD//BM)→���^=���^,���^=���^(��//��)
Mà AD=BM��=��
→ΔIAD=ΔIMB(g.c.g)→Δ���=Δ���(�.�.�)
→IA=IM,IB=ID→��=��,��=��
Lại có AE//CM→ˆEAI=ˆIMC��//��→���^=���^
Kết hợp AE=CM��=��
→ΔIAE=ΔIMC(c.g.c)→Δ���=Δ���(�.�.�)
→ˆAIE=ˆMIC→���^=���^
→ˆEIC=ˆAIE+ˆAIC=ˆMIC+ˆAIC=ˆAIM=180o→���^=���^+���^=���^+���^=���^=180�
→E,I,C→�,�,� thẳng hàng
→CE,AM,BD→��,��,�� đồng quy


Tứ giác ADMB có: AB//MD, AD//MB
ADMB là hình bình hành AB=MD và ˆDAB=ˆDMBDAB^=DMB^
Tứ giác ACME có: AE//MC, AC//ME
ACME là hình bình hành \Rightarrow AC=ME
Vì xy//BC nên ˆDAC=ˆACBDAC^=ACB^
mà ˆACB=ˆEMBACB^=EMB^ nên ˆDAC=ˆEMBDAC^=EMB^
Ta có: ˆDAB=ˆDMBDAB^=DMB^
ˆDAB−ˆDAC=ˆDMB−ˆEMBDAB^−DAC^=DMB^−EMB^
hay ˆBAC=ˆDMEBAC^=DME^
Tam giác ABC=MDE (c.g.c)

1)Các đường thẳng EM và MD cắt AB và AC lần lượt là K và H.
Kẻ đường thẳng EM,Ta có Vì EC//KM ta có HAMˆHAM^=AMEˆAME^(1)
Vì AB//MD=>KAMˆKAM^=AMDˆAMD^(2)
Mà BACˆBAC^=KAMˆKAM^+HAMˆHAM^(3)
tiếp KMDˆKMD^=KMAˆKMA^+AMDˆAMD^(4)
Từ (1),(2),(3) và (4)=>BACˆBAC^=EMDˆEMD^
Kẻ D với B.Xét tam giác ABD và tam giác MDB có:
DB là cạnh chung
MDBˆMDB^=DBAˆDBA^(vì MD//AB)
ADBˆADB^=DBMˆDBM^(vì xy//BC)
=>Tam giác ABD=Tam giác MDB(g.c.g)
=>DM=AB.
Kẻ E với C.Xét tam giác AEM và tam giác MCA có:
AM là cạnh chung
ACEˆACE^=CAMˆCAM^)(vì ME//AC)
EAMˆEAM^=AMCˆAMC^(vì xy//BC)
=>Tam giác AEM=Tam giác MCA(g.c.g)
=>ME=AC
Xét tam giác ABC và tam giác MDE có:
DM=AB(c/m trên)
ME=AC(c/m trên)
BACˆBAC^=EMDˆEMD^
=>Tam giác ABC=Tam giác MDE(c.g.c)
2)Thiếu điều kiện rồi.
Bài 6 mình sẽ bắt đầu bằng câu b nhé!
b)Vì MACˆMAC^+BAMˆBAM^=90o90o(gt)
Vì MACˆMAC^+CAEˆCAE^=90o90o(gt)
Từ trên=>CAEˆCAE^= BAMˆBAM^
Xét tam giác ABM và tam giác ACE có:
AB=BC(gt)
AM=AE(gt)
CAEˆCAE^= BAMˆBAM^(c/m trên)
=>Tam giác ABM=Tam giác ACE(c.g.c)
=>EC=BM(hai cạnh tương ứng)
c)Ta có: MABˆMAB^+MACˆMAC^=90o90o(gt)
Ta lại có tiếp: MABˆMAB^+BADˆBAD^=90o90o(gt)
=>BADˆBAD^=MACˆMAC^
Xét tam giác ADB và tam giác AMC có:
AB=AC(gt)
DA=AM(gt)
BADˆBAD^=MACˆMAC^(c/m trên)
=>Tam giác ADB=Tam giác AMC(c.g.c)
=>DB=MC(hai cạnh tương ứng)
Ta có BM+MC=BC(do M nằm giữa B và C)
Mà BM=EC(c/m trên)
DB=MC(c/m trên)
=>EC+DB=BC
d)Vì Tam giác ABM=Tam giác ACE(c/m trên)
=>ACEˆACE^=B^B^=45o45o(Vì góc B là góc ở đáy của tam giác vuông cân BAC tại A)
Vậy Ta có C^C^+ACEˆACE^=BCEˆBCE^=90o90o.(1)
Vì Tam giác ADB=Tam giác AMC(c/m trên)
=>C^C^=DBAˆDBA^=45o45o
Vậy B^B^+DBAˆDBA^=DBCˆDBC^=90o90o(2)
Từ (1) và (2)=>BCEˆBCE^= DBCˆDBC^=90o90o vậy BCEˆBCE^+DBCˆDBC^=180o180o mà hai góc này nằm ở vị trí trong cùng phía =>DB//EC

Ta có hình vẽ:
A B C I D E
Ta có: BI là pg góc B
=> góc DBI = góc IBC
Mà góc DIB = góc IBC (DE // BC)
=> góc DBI = góc DIB
=> tam giác BDI cân
=> BD = DI
Ta có: CI là phân giác góc C
=> góc ECI = góc ICB
Mà góc EIC = góc ICB (DE // BC)
=> góc ECI = góc EIC
=> tam giác CEI cân
=> CE = IE
Ta có: BD = DI; CE = IE
=> BD + CE = DI + IE
hay BD + CE = DE
hay DE = BD + CE
Ta có: DI // BC (gt)
Suy ra:∠I1 =∠B1(so le trong) (1)
Lại có:∠B1 =∠B2 (2)
(vì BI là yia phân giác góc B)
Từ (1) và (2) suy ra:∠I1 =∠B2
=>∆BDI cân tại D =>BD=DI (3)
Mà IE // BC (gt) =>∠I1 =∠C1 (so le trong) (4)
Đồng thời: ∠C1=∠C2 (vì CI là phân giác của góc C) (5)
Từ (4) và (5) suy ra: ∠C1=∠C2. Suy ra. ∠CEI cân tại E
Suy ra: CE = EI (hai cạnh tương ứng) (6)
Từ (3) và (6) suy ra: BD + CE = DI + EI = DE

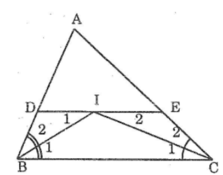
Ta có: DI // BC (giả thiết)
Suy ra:∠I1 =∠B1(so le trong) (1)
Lại có:∠B1 =∠B2 (2)
(vì BI là tia phân giác góc ABC)
Từ (1) và (2) suy ra:∠I1 =∠B2
=>∆BDI cân tại D =>BD=DI (3)
Mà IE // BC (gt) => ∠I2 =∠C1 (so le trong) (4)
Đồng thời: ∠C1=∠C2 (vì CI là phân giác của góc ACB) (5)
Từ (4) và (5) suy ra: ∠I2=∠C2. Suy ra ∠CEI cân tại E
Suy ra: CE = EI (6)
Từ (3) và (6) suy ra: BD + CE = DI + EI = DE