NM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
3
27 tháng 1 2015
\(\lim\limits_{x\rightarrow1}\frac{x^4+x^3-2}{x^5-x^2}=\lim\limits_{x\rightarrow1}\frac{x^4-1+x^3-1}{x^2\left(x^3-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{\left(x^2-1\right)\left(x^2+1\right)+\left(x-1\right)\left(x^2+x+1\right)}{x^2\left(x-1\right)\left(x^2+x+1\right)}\)\(=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left[\left(x+1\right)\left(x^2+1\right)+\left(x^2+x+1\right)\right]}{x^2\left(x-1\right)\left(x^2+x+1\right)}\)\(=\lim\limits_{x\rightarrow1}\frac{\left[\left(x+1\right)\left(x^2+1\right)+\left(x^2+x+1\right)\right]}{x^2\left(x^2+x+1\right)}\)=\(\frac{7}{3}\)
1 tháng 2 2018
=lim x^2(x^2+x) - 2 \ x^2(x^3-1)=lim(x^2+x)\(x^3-1)=lim 2\-2=-1
5 tháng 10 2015
ta có
\(y=\frac{\left(e^x+e^{-x}\right)\left(e^x+e^{-x}\right)-\left(e^x-e^{-x}\right)\left(e^x-e^{-x}\right)}{\left(e^x+e^{-x}\right)^2}=\frac{\left(e^x+e^{-x}\right)^2-\left(e^x-e^{-x}\right)^2}{\left(e^x+e^x\right)^2}=\frac{\left(e^x+e^{-x}+e^x-e^{-x}\right)\left(e^x+e^{-x}-e^x+e^{-x}\right)}{\left(e^x+e^{-x}\right)^2}=2\frac{e^x-e^{-x}}{\left(e^x+e^{-x}\right)^2}=\frac{2}{e^x+e^{-x}}\)
PT
1
CM
8 tháng 5 2018
Đáp án B
S n = 1 − 1 2 2 1 − 1 3 2 ... 1 − 1 n 2 = 1 − 1 2 1 − 1 3 ... 1 − 1 n × 1 + 1 2 1 + 1 3 ... 1 + 1 n
1 − 1 2 1 − 1 3 ... 1 − 1 n = 1 2 . 2 3 ... n − 1 n = 1 n 1 + 1 2 1 + 1 3 ... 1 + 1 n = 3 2 . 4 3 ... n + 1 n = n + 1 2 ⇒ S n = 1 n . n + 1 2 = n + 1 2 n lim S n = lim n + 1 2 n = lim 1 + 1 n 2 = 1 2
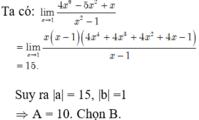
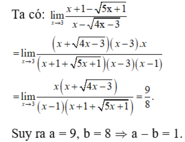
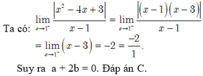
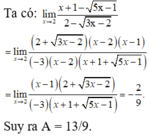
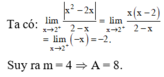
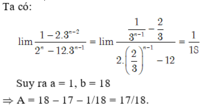
ta có:
\(\lim\limits_{x\rightarrow0}\frac{5^x-1}{20^x-1}=\lim\limits_{x\rightarrow0}\frac{\ln5.5^x}{\ln20.20^x}=\frac{ln5}{ln20}\)