Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

HẾT RỒI NHÉ ĐÁP ÁN LÀ :
+ Ta có: y '= 3x2 + 6x + m
+ Để hàm số đã cho đồng biến trên R thì y' ≥ 0,∀x ∈R
+ Yêu cầu bài toán trở thành tìm điều kiện của m để y' ≥ 0,∀x ∈R
Ta có y' = 3x2 + 6x + m, ta có: a = 3>0,Δ = 36 - 12m
Để y' ≥ 0,∀x ∈ R khi Δ ≤ 0 ⇔ 36 - 12m ≤ 0 ⇔ m ≥ 3
Vậy giá trị của tham số m cần tìm là m ≥ 3

đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.

1. a) Tập xác định : D = R; y' = 3 - 2x => y' = 0 ⇔ x = \(\dfrac{3}{2}\).
Bảng biến thiên :
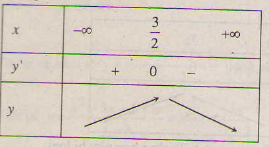
Hàm số đồng biến trên khoảng (-∞; \(\dfrac{3}{2}\)); nghịch biến trên khoảng ( \(\dfrac{3}{2}\); +∞ ).
b) Tập xác định D = R;
y'= x2 + 6x - 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên :
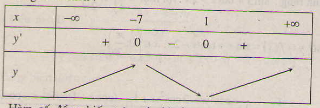
Hàm số đồng biến trên các khoảng (-∞ ; -7), (1 ; +∞) ; nghịch biến trên các khoảng (-7 ; 1).
c) Tập xác định : D = R.
y' = 4x3 - 4x = 4x(x2 - 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: tự vẽ.
Hàm số đồng biến trên các khoảng (-1 ; 0), (1 ; +∞) ; nghịch biến trên các khoảng (-∞ ; -1), (0 ; 1).
d) Tập xác định : D = R. y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = \(\dfrac{2}{3}\).
Bảng biến thiên :
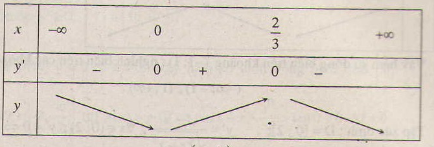
Hàm số đồng biến trên khoảng ( 0 ; \(\dfrac{2}{3}\) ) ; nghịch biến trên các khoảng (-∞ ; 0), ( \(\dfrac{2}{3}\); +∞).
1. a) Tập xác định : D = R; y' = 3 - 2x => y' = 0 ⇔ x = \(\dfrac{3}{2}\).
Bảng biến thiên :

Hàm số đồng biến trên khoảng (-∞; \(\dfrac{3}{2}\)); nghịch biến trên khoảng ( \(\dfrac{3}{2}\); +∞ ).
b) Tập xác định D = R;
y'= x2 + 6x - 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên :

Hàm số đồng biến trên các khoảng (-∞ ; -7), (1 ; +∞) ; nghịch biến trên các khoảng (-7 ; 1).
c) Tập xác định : D = R.
y' = 4x3 - 4x = 4x(x2 - 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: tự vẽ.
Hàm số đồng biến trên các khoảng (-1 ; 0), (1 ; +∞) ; nghịch biến trên các khoảng (-∞ ; -1), (0 ; 1).
d) Tập xác định : D = R. y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = 2323.
Bảng biến thiên :

Hàm số đồng biến trên khoảng ( 0 ; \(\dfrac{2}{3}\) ) ; nghịch biến trên các khoảng (-∞ ; 0), ( \(\dfrac{2}{3}\); +∞).

Lời giải:
TXĐ: $x\in\mathbb{R}$
$y'=3x^2+2x=0\Leftrightarrow x=0$ hoặc $x=\frac{-2}{3}$
Ta có bảng biến thiên:

Nhìn bảng ta thấy hàm só đồng biến trên $(-\infty; -\frac{2}{3})$ và $(0;+\infty)$; nghịch biến trên $(-\frac{2}{3};0)$

Gọi f(x)=x2+2x-3
\(f'\left(x\right)=2x+2\) \(\Rightarrow f'\left(x\right)=0\:\Leftrightarrow2x+2=0\:\Leftrightarrow x=-1\)
Vẽ bảng biến thiên giúp mình nghen. Từ \(\left(-\infty;-1\right)\)hàm số nghịch biến, từ \(\left(-1;+\infty\right)\) hàm số đồng biến.
Mà f(x)=0 \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Suy ra sẽ có 3 cực trị tại x=-3;x=1 và x=-1
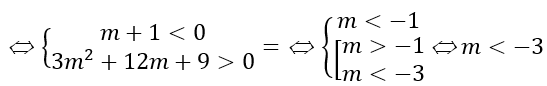
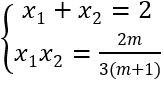
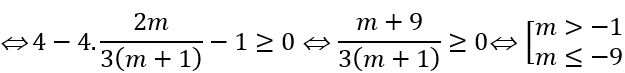


đáp án là :
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔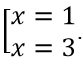
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔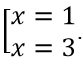
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
P/S : quá dễ , t là thần đồng mà .
Mỗi ngày 3 T i c k , giờ làm như lời hứa đi