HS
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dưới đây là một vài câu hỏi có thể liên quan tới câu hỏi mà bạn gửi lên. Có thể trong đó có câu trả lời mà bạn cần!
27 tháng 5 2018
\(\orbr{\begin{cases}x-\frac{13}{18}y=0\\x-\frac{18}{13}y=0\end{cases}}\)
CM
16 tháng 6 2018
Đáp án A
Phương án D không phải là hệ phương trình bậc nhất hai ẩn nên loại D
CM
19 tháng 9 2017
Hệ phương trình có chứa phương trình bậc hai là hệ phương trình ở đáp án D nên loại D
+ Với hệ phương trình A:
x − y = − 2 x + y = 4 ⇒ 1 − 3 = − 2 1 + 3 − 4 ⇔ − 2 = − 2 4 = 4 (luôn đúng) nên (1; 3) là nghiệm của hệ phương trình x − y = − 2 x + y = 4
+ Với hệ phương trình B: 2 x − y = 0 x + y = 4
Thay x = 1; y = 3 ta được 2.1 − 3 = 0 1 + 3 = 4 ⇔ − 1 = 0 1 + 3 = 4 (vô lý) nên loại B.
+ Với hệ phương trình C: x + y = 4 2 x + y = 4
Thay x = 1; y = 3 ta được 1 + 3 = 4 2.1 + 3 = 4 ⇔ 4 = 4 5 = 4 (vô lý) nên loại C.
Đáp án:A
30 tháng 5 2021
\(x^2-2x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}u=x_1+\left(x_2\right)^2\\v=x_2+\left(x_1\right)^2\end{matrix}\right.\)
\(\Rightarrow\)\(\left\{{}\begin{matrix}u+v=\left(x_1+x_2\right)+\left(x_2+x_1\right)^2-2x_1x_2\\uv=2x_1x_2+x_1^3+x_2^3=2x_1x_2+\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=8\\uv=12\end{matrix}\right.\)
=>u và v là nghiệm của pt \(t^2-8t+12=0\)
CM
19 tháng 9 2018
- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.
- Bạn Phương nhận xét sai.
Ví dụ: Xét hai hệ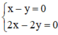 
và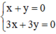 
Hệ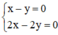 
có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
Hệ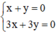 
có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.
NH
1
CM
8 tháng 2 2017
- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.
- Bạn Phương nhận xét sai.
Ví dụ: Xét hai hệ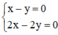 
và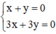 
Hệ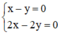 
có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
Hệ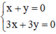 
có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.
Kiến thức áp dụng
Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.
Theo đề, ta có: ax+by=c
\(\Leftrightarrow\left\{{}\begin{matrix}2a=c\\a+2b=c\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{c}{2}\\b=\dfrac{1}{4}c\end{matrix}\right.\)
b=1/4c thì 1/4 ở đâu z