Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

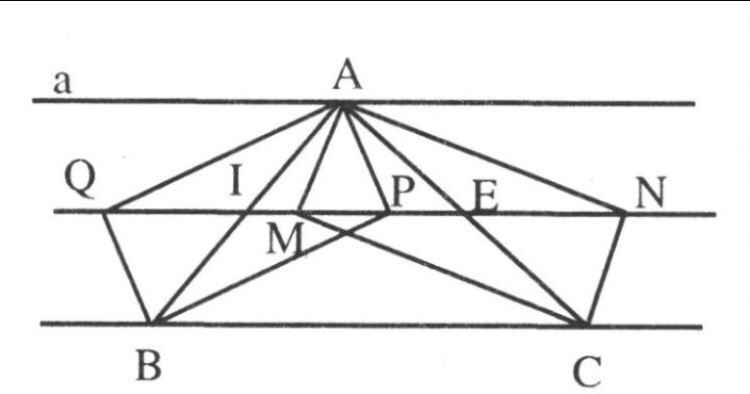
a. Vì BQ và BP là p/g ngoài và trong của \(\widehat{ABC}\) nên \(BP\bot BQ\)
Lại có \(AQ\bot BQ, AP\bot BP\) nên AQPB là hcn
Cmtt ta được AMCN cũng là hcn
b. Gọi I là giao 2 đường chéo AB và PQ của hcn AQBP
\(\Rightarrow IB=IA=IC\\ \Rightarrow\widehat{IPB}=\widehat{IBP}=\widehat{PBC}\left(BP\text{ là p/g}\right)\)
Mà 2 góc này ở vị trí slt nên IP//BC
\(\Rightarrow P,Q\) nằm trên đtb của \(\Delta ABC\)
Tương tự M,N cũng nằm trên đtb \(\Delta ABC\)
Vậy M,N,Q,P thẳng hàng

Tham khảo:
Đường phân giác ngoài tại một đỉnh của một tam giác là đường thẳng chia cạnh đối diện thàng hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy. Ví dụ: Trong tam giác ABC, có AD là phân giác ngoài của góc A và AD cắt BC tại D. Như vậy, ta có: DB/DC = AB/AC.
HT
TL:
Tham khảo: Đường phân giác ngoài tại một đỉnh của một tam giác là đường thẳng chia cạnh đối diện thàng hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy. Ví dụ: Trong tam giác ABC, có AD là phân giác ngoài của góc A và AD cắt BC tại D. Như vậy, ta có: DB/DC = AB/AC.
k cho mik nhé
@@@@@@@@@@@@@@@@@@@@@@@
HT

A B C N M E F G H I K
a) Kéo dài các tia AN; AE; AM; AF cho chúng cắt đường thẳng BC theo thứ tự tại các điểm G;H;I;K.
Xét \(\Delta\)ABI có: BM là phân giác ^ABI và BM vuông góc AI (tại M) => \(\Delta\)ABI cân tại B
=> BM đồng thời là đường trung tuyến \(\Delta\)ABI => M là trung điểm AI
C/m tương tự, ta có: N;E;F lần lượt là trung điểm của AG;AH;AK
Xét \(\Delta\)GAH: N là trung điểm AG; E là trung điểm AH => NE là đường trung bình \(\Delta\)GAH
=> NE // GH hay NE // BC (1)
Tương tự: MF // BC (2); NF // BC (3)
Từ (1); (2) và (3) => 4 điểm M;N;E;F thẳng hàng (Theo tiên đề Ơ-clit) (đpcm).
b) Theo câu a ta có: NF là đường trung bình \(\Delta\)AGK => \(NF=\frac{GK}{2}=\frac{BG+BC+CK}{2}\)(*)
Lại có: \(\Delta\)ABG cân ở B; \(\Delta\)ACK cân ở C (câu a) nên BG = AB; CK = AC
Thế vào (*) thì được: \(NF=\frac{AB+BC+AC}{2}\),
KL: ...