Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Khoảng vân ứng với ánh sáng đỏ là i i = 0 , 4 . 10 - 6 . 3 3 . 10 - 3 = 0 , 4 . 10 - 3 ( m ) = 0,40mm.
Bề rộng của quang phổ thứ nhất là d = 0,75mm – 0,40mm = 0,35mm.

Phương pháp:
Quang phổ ngay sát vạch sáng trung tâm là quang phổ bậc 1
Công thức tính bề rộng quang phổ bậc n : ∆xn = xđn - xtn
Cách giải:
Bề rộng quang phổ bậc 1 là:
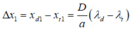
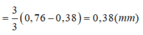
Đáp án A

Bề rộng quang phổ liên tục bậc 3 là
\(L = x_{đỏ}^k-x_{ tím}^k= 3\frac{D}{a}(\lambda_d-\lambda_t)=2,85mm.\)
Với \(D = 2m; a= 0,8mm; \lambda_d = 0,76 \mu m; \lambda_t = 0,38 \mu m.\)

Tại vị trí cách vân trung tâm 3 mm có vân sáng bậc \(k\) của bức xạ \(\lambda\) khi
\(x=3mm = ki =k\frac{\lambda D}{a}.\)
=> \(\lambda = \frac{3.a}{D k}.(1)\)
Mặt khác : \(0,38 \mu m \leq \lambda \leq 0,76 \mu m.\)
<=> \(0,38 \mu m \leq \frac{3a}{kD} \leq 0,76 \mu m.\)
<=> \(\frac{3.0,8}{0,76.2} \leq k \leq \frac{3.0,8}{0,38.2} \)
Giữ nguyên đơn vị của \(x = 3mm; a = 0,8mm;\lambda = 0,76 \mu m;0,38 \mu m; D= 2m\)
<=> \(1,57 \leq k \leq 3,15.\)
<=> \(k = 2,3.\)
Thay vào (1) ta thu được hai bước sóng là \(\lambda_1 = \frac{3.0,8}{2.2}=0,6\mu m.\)
\(\lambda_2 = \frac{3.0,8}{3.2}=0,4\mu m.\)

Chọn C.
Khoảng vân i = 0,2mm, vị trí vân sáng bậc 3 (với k = 3) là x3 = 3.i = 0,6mm.
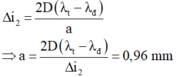

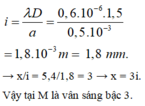
Chọn C.
→ bề rộng của quang phổ thứ hai là
d = xđỏ 2 - xtím 2 = 2.iđỏ -2.itím = 2.0,75mm – 2.0,40mm = 0,7mm