Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì nói chung a và b không song song với nhau vì a và b có thể cắt nhau hoặc có thể chéo nhau.
b) Trong không gian nếu a ⊥ b và b ⊥c thì a và c vẫn có thể cắt nhau hoặc chéo nhau do đó, nói chung a và c không vuông góc với nhau.

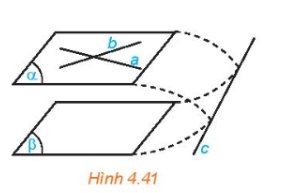
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.

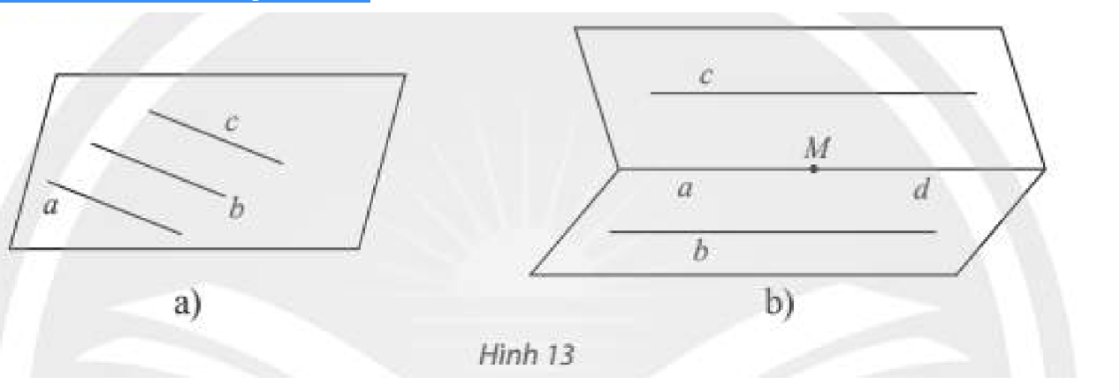
Ta có: \(d = mp\left( {a,c} \right) \cap mp\left( {M,b} \right) \Rightarrow M \in d\)
Lại có: \(M \in a\)
Mà qua \(M\) chỉ có một đường thẳng song song với đường thẳng \(b\) nên \(d \equiv a\).
Do đó \(a\parallel b\).

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

Không vì trái với định lí ( a // b thì a và b không cắt nhau)
Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì nói chung a và b không song song với nhau vì a và b có thể cắt nhau hoặc có thể chéo nhau.