Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(n\left(\Omega\right)=C^4_8\cdot C^4_4\)
X: "2 bạn Việt và Nam nằm chung 1 bảng"
Số cách xếp là:
\(n\left(X\right)=C^1_2\cdot C^2_6\cdot C^4_4\)
=>P=3/7

Đáp án B
Số phần tử của không gian mẫu là: ![]()
Gọi X là biến cố “cả hai bạn Việt và Nam nằm chung một bảng đấu’
Số kết quả thuận lợi cho biến cố X là: ![]()
Vậy xác suất cần tính
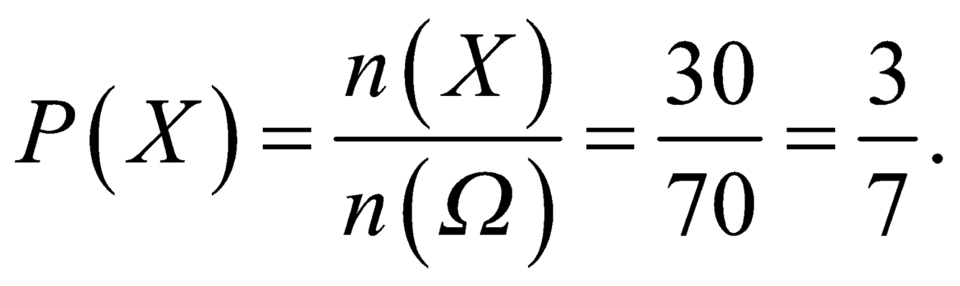

\(C=M\cup N\)
\(D=M\cap N\)
\(F=M\cap\overline{N}\)
\(G=\left(\overline{N}M\right)\cup\left(\overline{M}N\right)\)

Chọn B.
Số phần tử của không gian mẫu:
![]()
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: ![]()
![]() .
.

Chọn B
Gọi 2 cặp vợ chồng là C1-V1 và C2-V2 (C=chồng, V=vợ).
* Số cách chọn ra 7 đôi:
- Đầu tiên chọn ra 7 nam trong 10 nam: C 10 7 (cách).
- Xếp 7 người nam này thành 1 hàng ngang, người đầu tiên có 12 cách ghép với nữ, người thứ hai có 11 cách, cứ như thế suy ra số cách ghép đôi là 12.11.10.9.8.7.6 (cách).
- Theo quy tắc nhân có 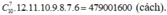
* Số cách chọn 7 đôi, chỉ có một cặp vợ chồng
- Trường hợp 1: chỉ có cặp vợ chồng C1-V1, khi đó lấy 6 nam trong 9 nam còn lại:
+ Nếu trong 6 nam này không có C2 thì số cách ghép 6 cặp còn lại là: ![]()
+ Nếu trong 6 nam này có C2 thì số cách ghép 6 cặp còn lại là: có 10 cách ghép C2 với nữ (trừ V2 và trừ V1), 5 nam còn lại có cách, số cách ghép cặp cho 5 nam này là 10.9.8.7.6 cách. Vậy theo quy tắc nhân có ![]()
Theo quy tắc cộng, có ![]()
- Trường hợp 2: chỉ có cặp vợ chồng C2-V2, tương tự như trên có 26248320(cách)
Vậy xác suất cần tính là: ![]()

Số vận động viên được khảo sát là \(n = 3 + 8 + 12 + 12 + 4 = 39\).
Gọi \({x_1};{x_2};...;{x_{39}}\) là thời gian luyện tập của 39 vận động viên được xếp theo thứ tự không giảm. Ta phải chọn các vận động viên có thời gian luyện tập tương ứng là \({x_{30}};{x_{31}};...;{x_{39}}\)
Ta có:
\({x_1},{x_2},{x_3} \in \left[ {0;2} \right);{x_4},...,{x_{11}} \in \left[ {2;4} \right);{x_{12}},...,{x_{23}} \in \left[ {4;6} \right);{x_{24}},...,{x_{35}} \in \left[ {6;8} \right);{x_{36}},...,{x_{39}} \in \left[ {8;10} \right)\). Vậy \({x_{30}}\) thuộc nhóm \(\begin{array}{*{20}{l}}{\left[ {6;8} \right)}\end{array}\).
Ta có: \(n = 29;{n_j} = 12;C = 3 + 8 + 12 = 23;{u_j} = 6;{u_{j + 1}} = 8\)
\({x_{30}} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 6 + \frac{{\frac{{3.39}}{4} - 23}}{{12}}.\left( {8 - 6} \right) \approx 7,04\)
Vậy huấn luyện viên nên chọn các vận động viên có thời gian luyện tập từ 7,04 giờ trở lên.

Đáp án B
Gọi A là biến cố xảy ra trường hợp để yêu cầu.Không gian mẫu
![]()
Xét các trường hợp có thể xảy ra biến cố A là.
+) 2 nam Toán, 2 nữ Lý: C 8 2 . C 7 2 = 588
+) 2 nữ Toán, 2 nam Lý: C 7 2 . C 5 2 = 210
+) 1 nam Toán, 1 nam Lý, 1 nữ Toán, 1 nữ Lý
C 7 1 . C 5 1 . C 7 1 . C 8 1 = 1960
Số cách chọn cần tìm
![]()
Xác suất cần tìm là. 197 495





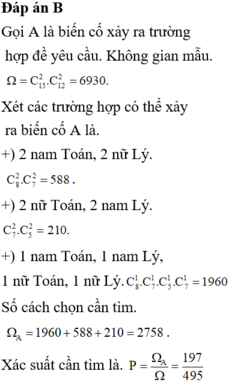
Tổng số trận đấu của các vận động viên: \(C_{3n}^2\)
Gọi số trận thắng của nữ là x thì của nam là \(_{C_{3n}^{ }^2}\)- x
Lập tỉ số và đưa về pt: 8.x = 7.n.(3n-1)
Vậy n(3n-1) phải chia hết cho 8, do đó n=3, 11, ......
Tùy theo đáp án của trắc nghiệm mà các bạn chọn đáp số.