Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
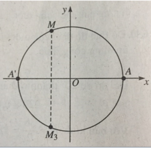
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
\(B=cos\frac{\pi}{7}.cos\left(\pi-\frac{4\pi}{7}\right).cos\left(\pi-\frac{2\pi}{7}\right)\)
\(B=cos\frac{\pi}{7}.cos\frac{2\pi}{7}.cos\frac{4\pi}{7}\)
\(B.sin\frac{\pi}{7}=sin\frac{\pi}{7}.cos\frac{\pi}{7}.cos\frac{2\pi}{7}.cos\frac{4\pi}{7}\)
\(B.sin\frac{\pi}{7}=\frac{1}{2}sin\frac{2\pi}{7}.cos\frac{2\pi}{7}.cos\frac{4\pi}{7}\)
\(B.sin\frac{\pi}{7}=\frac{1}{4}sin\frac{4\pi}{7}.cos\frac{4\pi}{7}=\frac{1}{8}sin\frac{8\pi}{7}\)
\(B.sin\frac{\pi}{7}=\frac{1}{8}sin\left(\pi+\frac{\pi}{7}\right)=-\frac{1}{8}sin\frac{\pi}{7}\)
\(\Rightarrow B=-\frac{1}{8}\)
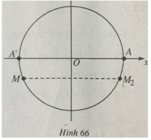
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
\(A=\frac{1}{2}+\frac{1}{2}cos2x+\frac{1}{2}+\frac{1}{2}cos\left(2x+\frac{4\pi}{3}\right)+\frac{1}{2}+\frac{1}{2}cos\left(2x-\frac{4\pi}{3}\right)\)
\(=\frac{3}{2}+\frac{1}{2}cos2x+cos2x.cos\frac{4\pi}{3}\)
\(=\frac{3}{2}+\frac{1}{2}cos2x-\frac{1}{2}cos2x=\frac{3}{2}\)
\(B=\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos\left(2x+\frac{4\pi}{3}\right)+\frac{1}{2}-\frac{1}{2}cos\left(2x-\frac{4\pi}{3}\right)\)
\(=\frac{3}{2}-\frac{1}{2}cos2x-cos2x.cos\frac{4\pi}{3}\)
\(=\frac{3}{2}-\frac{1}{2}cos2x+\frac{1}{2}cos2x=\frac{3}{2}\)
Lời giải:
$\cos^2 a=1-\sin^2a=1-(\frac{3}{5})^2=\frac{16}{25}$
$\Rightarrow \cos a=\pm \frac{4}{5}$
Ta có:
\(\cos (a-\frac{\pi}{3})=\cos a\cos \frac{\pi}{3}-\sin a\sin \frac{\pi}{3}\)
\(=\frac{1}{2}\cos a-\frac{3\sqrt{3}}{10}=\frac{1}{2}.\pm \frac{4}{5}-\frac{3\sqrt{3}}{10}\)
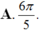
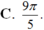
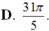
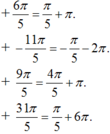
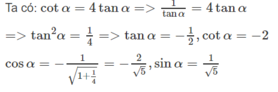
Đáp án: B
Ta có:
Vậy hai góc lượng giác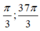
có cùng tia đầu và tia cuối trên đường tròn lượng giác.